Maths.net

Quatrième Géométrie euclidienne Les triangles Généralités Définition : un triangle est un polygone à trois côtés. Définition : il existe 4 types de triangle dont 3 types particuliers : quelconque, sans particularités, isocèle avec 2 côtés égaux, équilatéral avec 3 côtés égaux et rectangle avec un angle droit. Propriété : la somme des mesures des angles d'un triangle fait 180°. Propriété : Dans un triangle, la droite passant par les milieux de deux côtés opposés est parallèle au troisième côté et mesure la moitié de celui-ci. Droites dans le triangle. Définition : La médiane issue d'un sommet est la droit passant par ce sommet et le milieu du côté opposé. La hauteur issue d'un sommet est la droite passant par ce sommet et perpendiculaire au côté opposé. 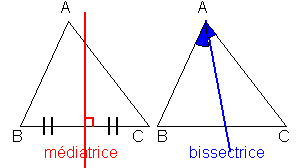La médiatrice d'un segment est la droite passant par le milieu de ce segment et perpendiculaire à celui ci. La bissectrice d'un angle est la droite coupant celui ci en deux angles égaux faisant chacun la moitié de l'angle initial. Propriétés : Les trois médianes se coupent en un point appelé le centre de gravité du triangle. Les trois hauteurs se coupent en un point appelé l'orthocentre du triangle. Les trois médiatrices se coupent en un point qui est le centre du cercle circonscrit au triangle, c'est à dire le cercle passant par les trois sommets du triangle. Les trois bissectrices se coupent en un point qui est le centre du cercle inscrit du triangle, c'est à dire le cercle tangent aux trois côtés du triangle. 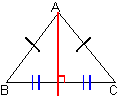Propriétés des triangles particuliers Propriétés du triangle isocèle Dans un triangle ABC isocèle en A, la médiane, la hauteur, la bissectrice issues de A et la médiatrice de la base [BC] sont confondues. Les deux angles à la base d'un triangle isocèle ont même mesure. (la réciproque est vraie) Propriétés du triangle équilatéral : Dans un triangle ABC équilatéral, la médiane, la hauteur, la bissectrice issues d'un sommet et la médiatrice du côté opposé sont confondues. Il vient que l'orthocentre, le centre de gravité, le centre du cercle circonscrit et le centre du cercle inscrit sont confondus. Les angles d'un triangle équilatéral ont même mesure, c'est à dire 60°. 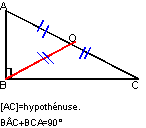Propriétés du triangle rectangle Dans un triangle rectangle, l'hypoténuse est le côté le plus grand du triangle, et la médiane relative à l'hypoténuse mesure la moitié de l'hypoténuse. (la réciproque est vraie). Le cercle circonscrit à un triangle rectangle a pour diamètre l'hypoténuse, le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse (la réciproque est vraie). Dans un triangle rectangle, les angles aigus sont complémentaires (leur somme fait 90°) Retour