| Lycée. Epreuve Finale
|
Site universitaire scientifique de Mont-Saint-Aignan

|
A la découverte du campus. Fiche 4
Mathématiques
|
Pour une case, cliquer dedans, puis saisir la réponse avec le clavier.
Attention à l'orthographe!
 Question 1 Question 1
Dans quelle théorie, les chercheurs du Laboratoire de Mathématiques Raphaël Salem étudient-ils la "transformation du boulanger"?
Réponse: La théorie:
Explications:
Site de recherche: www.univ-rouen.fr/LMRS/Vulgarisation/TE/img0.html
La théorie ergodique est l'étude des systèmes dynamiques du point de vue de la théorie de la mesure. Il s'agit de décrire les propriétés de systèmes qui évoluent tout en conservant un certain équilibre statistique. La théorie ergodique est un lieu de rencontre de divers domaines mathématiques: probabilités, géométrie, théorie des nombres, théorie classique des systèmes dynamiques.

 Question 2 Question 2
Quand les mathématiciens parlent de brûlage d'un arbre, de quel type d'arbre s'agit-il?
Réponse: Il s'agit d'un arbre
Explications:
Le brûlage des arbres binaires intervient dans les théories mathématiques qui tentent d'expliquer la formation des avalanches ou la constitution des dunes de sables.

 Question 3 Question 3
En quelle année a été publié le plus vieux livre que possède la bibliothèque du laboratoire de Mathématiques de l'Université de Rouen?
Réponse:
Explications:
Le plus vieux livre que possède la bibliothèque du laboratoire de Mathématiques de l'Université de Rouen est le dictionnaire de mathématiques de Hippolyte Sonnet (Inspecteur de l'Académie de la Seine, docteur es-sciences, professeur adjoint à l'Ecole Centrale des Arts et Manufactures).

 Question 4 Question 4
On appelle trisectrices les deux demi-droites qui partagent un angle en trois angles égaux. Certaines intersections des trisectrices d'un triangle quelconque constituent les sommets d'un triangle équilatéral.
Comment nomme-t-on ce triangle? |
|
Réponse: Triangle de
Explications:
Sites de recherche: http://www.reunion.iufm.fr/dep/mathematiques/abracadabri/GeoPlane/Classiques/Morley/Morley1.htm
http://users.skynet.be/radoux/morley.htm
Il s'agit là d'une propriété du triangle qui a été découverte tardivement par Frank MORLEY (1860-1937), mathématicien anglo-américain. Il n'existe pas de démonstration très simple de cette propriété. Récemment, le mathématicien français Alain CONNES en a proposée une un peu moins complexe que les autres.
Références: Alain CONNES : A new proof of Morley's theorem, Quadrature 47, 2003, pp 29-31
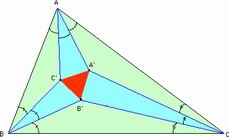
Triangle (et théorème) de Morley: On considère un triangle quelconque ABC et on suppose réalisées les trisections des angles A, B et C comme indiqué ci-dessus. Dans ces conditions, le triangle A'B'C' est équilatéral.

 Question 5 Question 5
Les mathématiciens ont donné le nom de Salem à certains nombres plus grands que 1.
Donner avec 5 décimales une valeur approchée du plus petit nombre de Salem connu.
Réponse:
Explications:
Site de recherche: http://www.univ-rouen.fr/LMRS/Salem/nbressalem.pdf
On peut consulter le mémoire de DEA de Christophe Doche qui précise (p17) que le plus petit nombre de Salem connu vaut approximativement 1,1762808. C'est la plus grande racine réelle du polynôme .
Références: Marie-José BERTIN : Problèmes de Lehmer, nombres de Pisot et de Salem, Quadrature 29, 1997, pp 26-32

 Question 6 Question 6
Seuls trois nombres entiers inférieurs à 100 peuvent se décomposer de deux manières différentes comme sommes de deux carrés d'entiers non nuls.
Que valent ces trois nombres?
Réponse: Dans l'ordre croissant: ; et
Explications:
Site de recherche: http://membres.lycos.fr/villemingerard/Addition/Partiti1.htm#Carré
; ;
Retour
|
|
|