| Quatrième
|
| Algèbre
|
| Les équations
|
1) Du type x+b=c ou x-b=c
Il faut isoler x à gauche de l'égalité. La propriété principale que l'on utilise dans les équations est celle ci:
Propriété: Dans une égalité, lorsque l'on effectue une opération à droit, il faut l'effectuer à gauche.
On a donc:
| x+b=c |
x-b=c |
x+b-b=c-b
x=c-b |
x-b+b=c+b
x=c+b |
A savoir : Une addition devient une soustraction et une soustraction devient une addition.
2) Du type ax=b ou x/a=b
Ici on veut faire disparaître le 'a' à gauche pour isoler x.
On a donc ,
D'où , x = ab
A savoir : une multiplication devient une division et une division devient une multiplication.
3) Du type 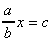
Ici deux méthodes: soit on considère que l'on a une multiplication (par a) puis une division (par b) et on utilise la méthode vue ci dessus. Soit on considère que l'on a une grande multiplication par a / b.
1. 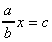 donne donne 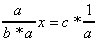 donc donc 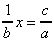 d'où d'où 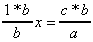
et enfin : 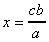
2. 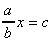 donne donne 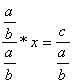 et donc : et donc : 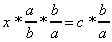
et enfin : 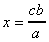
En fait, il faut savoir qu'une division de fraction revient à multiplier par l'inverse de celle ci.
Une astuce: ce qu'on a en haut on l'envoie en bas et ce qu'on a en bas on l'envoie en haut. (multiplication seulement)
4) Du type 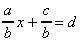 ou ax+b=c (même chose) ou ax+b=c (même chose)
Tout d'abord il faut toujours éliminer les additions et les soustractions par rapport à l'inconnue 'x'. Puis on s'occupe des multiplications et des divisions.
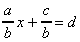 donne: donne: 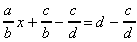 d'où d'où 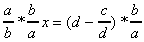 donc donc 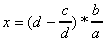
De même : ax+b=c donne ax+b-b=c-b d'où ax=c-b et 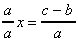
Donc 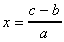
5) Du type (ax+b) (cx+d) = 0
Equations vues en 3éme. Propriété: Un produit de facteurs est nul si et seulement si un des facteurs est nul.
Donc (ax+b) (cx+d) = 0 si et seulement si : ax+b=0 ou cx+d=0 et ça on sait résoudre (voir plus haut). Cela nous donne donc deux solutions.
6) Du type
Ici on utilise les racines carrées et on a x*x=b/a et donc:
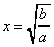 ou bien ou bien 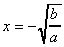 . .
Retour
|
|
|