| Quatrième
|
| Trigonométrie
|
| Vecteurs dans le plan
|
Définitions
Définition: Un vecteur est défini par trois composantes:
- Sa direction: celle de la droite qui porte le vecteur.
- Son sens: oriente le vecteur (par la flèche) exemple:
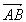 sens de A vers B. sens de A vers B.
- Sa longueur (norme en physique): il suffit de mesurer.
Remarque: De ce fait, un vecteur peut être déplacé n'import où dans le plan à condition que ses trois composantes, direction, sens et longueur ne changent pas.
Propriétés:
- Deux vecteurs sont égaux si et seulement si ils ont même direction, même sens et même longueur.
- Si
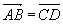 alors ABDC est un parallélogramme. alors ABDC est un parallélogramme.
2) Opérations sur les vecteurs
Somme: Soit 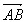 et et 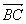 deux vecteurs, alors deux vecteurs, alors 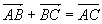 qui est la diagonale issue du parallélogramme formé par les vecteurs qui est la diagonale issue du parallélogramme formé par les vecteurs 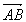 et et 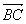 (cf. dessin). (cf. dessin).
Remarque: Pour 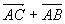 (les deux vecteurs issus d'un même point), on utilise la même méthode. (les deux vecteurs issus d'un même point), on utilise la même méthode.
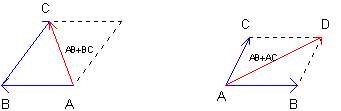
Relation de Chasles: Pour tous points A, B, C, on a : 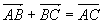 . En pratique (à ne pas mettre sur une copie) le point à droit du premier vecteur doit être le même que le point à gauche du second vecteur. . En pratique (à ne pas mettre sur une copie) le point à droit du premier vecteur doit être le même que le point à gauche du second vecteur.
Vecteurs opposés: Soit 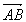 un vecteur, on note un vecteur, on note 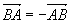 le vecteur opposé à le vecteur opposé à 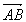 . En pratique, . En pratique, 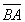 est de sens contraire à est de sens contraire à 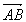
Remarques:
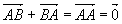 vecteur nul (d'après Chasles) vecteur nul (d'après Chasles)
- Soustraire deux vecteurs revient à additionner l'un avec l'opposé du second:
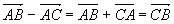
3) Colinéarité, multiplication par un réel
Définition: Soit un vecteur 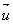 et k un réel. Le vecteur et k un réel. Le vecteur 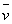 résultat de la multiplication de k par résultat de la multiplication de k par 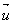 est: est:
- Si k=0,
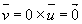
- Si k>0,
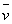 et et 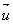 ont même sens, même direction mais sont de longueurs différentes. ont même sens, même direction mais sont de longueurs différentes.
- Si k<0,
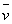 et et 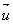 ont même direction, mais sont de sens opposés et n'ont pas même longueur. ont même direction, mais sont de sens opposés et n'ont pas même longueur.
Propriétés:
Colinéarité: Deux vecteurs 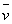 et et 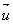 sont colinéaires si et seulement si! sont colinéaires si et seulement si!
L'un des vecteurs est nul.
Il existe un réel k tel que 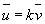
Propriétés:
- 3 points A, B, C sont alignés si et seulement si
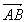 et et 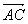 sont colinéaires. sont colinéaires.
- Si deux droits (AB) et (CD) sont parallèles, alors
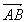 et et 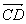 sont colinéaires. sont colinéaires.
- Inversement, si
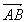 et et 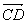 sont colinéaires, alors les droits (AB) et (CD) sont parallèles ou confondues. sont colinéaires, alors les droits (AB) et (CD) sont parallèles ou confondues.
Retour
|
|
|