| Troisième
|
| Algèbre
|
| Inéquations et systèmes d'inéquations
|
Propriétés des inégalités
Addition et soustraction: Pour tous réels a, b, c avec a<b (respectivement a>b) alors:
(respectivement )
(respectivement )
Multiplication et division: soient a et b réels tels que a<b (respectivement a>b) alors
Si c>0 alors (respectivement )
Si c<0 alors (respectivement )
Pour la division, pas de changement par rapport à la multiplication.
Propriété: Quand on multiplie (ou divise) les membres d'une inégalité par un nombre négatif, on change le signe de l'inégalité.
Résolution d'inéquations
La résolution d'inéquations est sensiblement la même que la résolution d'équations. Il faut faire attention aux changements de signes des inégalités lors de la présence de nombres négatifs. Exemple:
On trace les solutions sur une droite graduée ou on les présente sous forme d'intervalle:
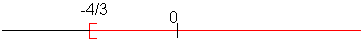
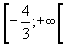
3) Résolution de système d'inéquations à une inconnue
Résoudre les 2 inéquations séparement, confronter sur une même droite si possible les solutions des 2 inéquations:
Exemple: 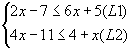
L1 donne 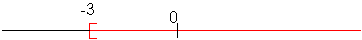
L2 donne 
La confrontation des solutions donne: S=[-3;5] ou encore:

4) Résolution (graphique) de systèmes d'inéquations à deux inconnues
Tracer les deux droits correspondantes aux deux inégalités; exemple:
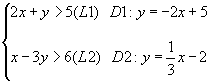 et le système devient et le système devient 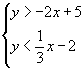
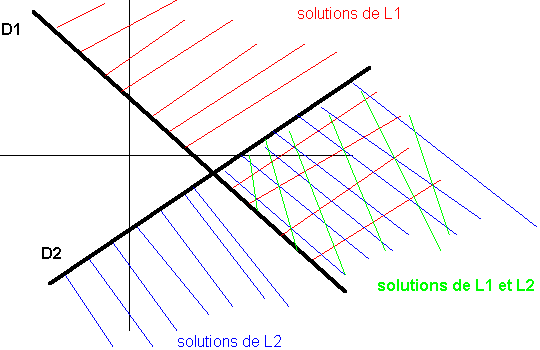
- Si le signe de l'inéquation est ">" les couples (x,y) solutions sont situés au dessus de la droite.
- Si le signe de l'inéquation est "<" les couples (x,y) solutions sont situés au dessous de la droite.
- Si le signe égale est compris, alors on inclut aussi la droite dans les solutions.
- Les couples solutions du système sont ceux vérifiant à la fois la première et la deuxième inéquation.
Ici cela nous donne:
Retour
|
|
|