Maths.net

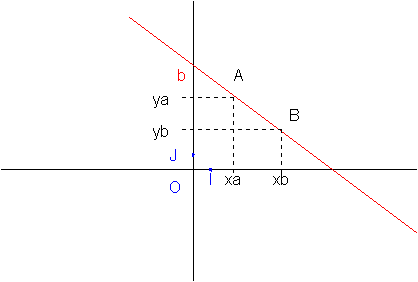
Troisième Géométrie analytique Equations de droites Définition Définition: Soit un repère orthonormé (O,I,J), alors toute droite admet une équation du type y=ax+b dans ce repère avec a le coefficient directeur (ou pente) de la droite et b l'ordonnée à l'origine. Remarque: l'ordonnée à l'origine est le point d'intersection de la droite avec l'axe des ordonnées. Pour les puristes: en fait une droite a comme équation ax+by+c=0. L'équation du type y=dx+e découle de la première à condition que b soit différent de 0 (Programme de Seconde). Définition: soit A(xa,ya) et B(xb,yb) alors le coefficient directeur de la droite (AB) est défini par : 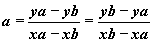2) Propriétés Toute droite parallèle à l'axe Ox admet une équation du type y=k Toute droite parallèle à l'axe Oy admet une équation du type x=k Si deux droites d:y=ax+b et d':y=a'x+b' sont parallèles, alors a=a' Si deux droites d et d' sont perpendiculaires, alors a*a'=-1 (réciproque vraie) 3) Calcul de l'équation d'une droite Avec deux points A(xa,ya) et B(xb,yb): On résout le système de deux équation à deux inconnues (a,b): 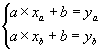On calcule le coefficient directeur grâce à la formule et on résout une équation à une inconnue: b Avec un point et le coefficient directeur, on est ramené à trouver b avec une équation à une inconnue. Avec un point et l'ordonnée à l'origine, idem que ci dessus sauf que là il faut trouver a. Retour