Maths.net

Seconde Algèbre Valeurs absolues ? encadrements Définition et propriétés Définition: soit x un réel, on appelle valeur absolue de x notée | x | le nombre positif défini par: | x | = x si x est positif. 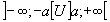| x | = -x si x est négatif Propriétés: Si y est non nul, Inégalité du triangle: Propriétés: soit a>0 et x réel alors: | x | = a équivaut à x=a ou x=-a | x | < a équivaut à S=]-a;a[ | x | > a équivaut à S= Encadrements Définition: Réaliser l'encadrement d'un nombre x quelconque, c'est trouver deux nombres a et b tels que a<x<b. L'amplitude de l'encadrement est c=b-a. Valeur approchée: soient a et x deux nombres et e>0. Alors a est une valeur approchée de x (ou approximation) à e près (ou à la précision de e près) quand Définition: Soient a, x des réels et e>0, A est une valeur approchée de x à e près par défaut si a<x<a+e A est une valeur approchée de x à e près par excès si a-e<x<a Propriétés: Soit x tels que et , une valeur approchée de x est c=(a+b)/2. La précision est e=(b-a)/2 et c est une valeur approchée de x à e près soit Si x tel que et et que et et alors on a et et et Si x tel que et , un majorant de | x | est le plus grand nombre en valeur absolue de | a | ou | b |. Retour