Maths.net

Seconde Algèbre Fonctions ? tableaux de signes Définitions Définition intervalles: On appelle intervalle I=[a,b] avec a<b les nombres compris entre les bornes de celui ci. On distingue les intervalles ouverts (les bornes ne sont pas comprises) et fermés (les bornes sont comprises). I=[a,b] intervalle fermé en a et b.: x appartient à I équivaut à et I=[a,b[, intervalle fermé en a et ouvert en b, x appartient à I équivaut à et I=]a,b], intervalle fermé en b et ouvert en a, x appartient à I équivaut à I=]a,b[, intervalle ouvert en a et b, x appartient à I équivaut à et Définition de fonctions: on appelle f(x) sur un intervalle [a,b] l'image de tous les points x appartenant à [a,b] par l'expression définie par f. On l'appelle fonction de x noté f(x) ou 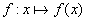. Dans le plan, f(x)=y situé sur l'axe des ordonnées. Exemple: f(x)=2x+3=y. x est l'antécédent de y par la fonction f. 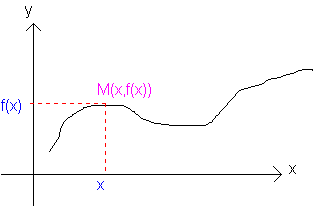Définition graphe: On appelle la courbe sur [a,b] représentée par la jonction de tous les points M(x,f(x)). C'est la courbe représentative de f sur [a,b]. 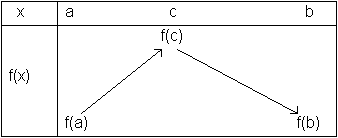Sens de variation d'une fonction Définition: Etudier le sens de variation d'une fonction correspond à regarder les variations (décroissance, constance, croissance) de la courbe donc de la fonction f(x): Tableau de variation: c'est un tableau récapitulant les variations de la fonction f sur un intervalle donné [a,b]. (exemple ci dessus). Extremums d'une fonction: on appelle extremum d'une fonction f, la valeur minimale ou maximale de f(x) sur l'intervalle d'étude. Tableaux de signes Etude du signe d'une fonction: soit une fonction f(x), pour étudier le signe de f, on étudie le signe de chaque facteur de f. Exemple: f(x)=2x(x+3)(x-5) Trouver les valeurs qui annulent chaque facteur. Dans notre exemple: 2x=0 équivaut à ; x+3=0 équivaut à ; x-5=0 équivaut à . Trouver le signe de chaque facteur de f de part et d'autre de chaque qui annule ceux ci. Dans notre exemple: 2x: positif pour , négatif pour . x+3 positif pour =-3, négatif pour =-3. x-5 positif pour =5 et négatif pour =5 Tracer le tableau de signes avec les différents facteurs de f dans la première colonne et f(x) à la fin. Pour trouver le signe de f(x), on additionne le nombre de signes "-" dans chaque colonne, si cette somme est impaire, le signe résultant est "-", sinon c'est "+". x     2x -   - 0 +   + X+3 - 0 +   +   + x-5 -   -   - 0 + F(x) - 0 + 0 - 0 + On trouve le signe de f(x): f(x)>0 pour f(x)<0 pour f(x)=0 pour x=-3, x=0 et x=5 NB ? A savoir: si f(x) est un quotient, les valeurs qui annulent le dénominateur ne sont pas définies pour f(x) (cas où on met une double barre dans le tableau de signes et/ou de variation). Retour