| Seconde
|
| Géométrie
|
| Cercle trigonométrique - radians
|
Définitions
Définition: Soit (C) un cercle de rayon 1 et de centre O. On décide de l'orienter dans le sens inverse des aiguilles d'une montre qu'on qualifiera de sens positif (ou sens direct). Ce cercle est appelé cercle trigonométrique.
Définition: Soit 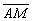 un arc du cercle trigonométrique (de rayon 1) la mesure en radians de l'arc un arc du cercle trigonométrique (de rayon 1) la mesure en radians de l'arc 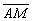 est égale à la longueur de celui ci. est égale à la longueur de celui ci.
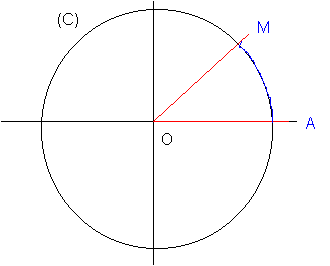
2) Mesures d'angles en radians
Propriété: soit le cercle trigonométrique (C) orienté dans le sens direct. Son périmètre est alors de . On a donc la mesure du cercle en radian égale à équivalent à un angle de 360°. On peut donc trouver la mesure en radian d'un arc sachant l'angle formé par celui ci.
Propriété: soit a la mesure d'un arc 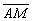 en radians, alors toutes les mesure de cet arc sont de la forme: en radians, alors toutes les mesure de cet arc sont de la forme: 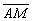 , avec . (en effet, revient à k fois le périmètre du cercle). , avec . (en effet, revient à k fois le périmètre du cercle).
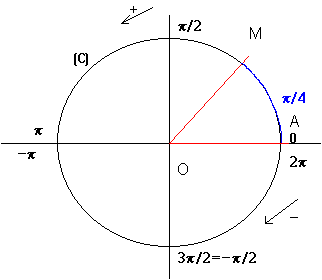
Définition: On appelle mesure principale en radians d'un arc 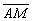 orienté, l'unique valeur de la mesure de cet arc comprise dans l'intervalle orienté, l'unique valeur de la mesure de cet arc comprise dans l'intervalle
Remarque: on peut donc mesurer un arc en partant dans le sens inverse du sens direct, la mesure de cet arc sera alors négative (cf dessin).
Définition: on appelle angle orienté de deux vecteurs et l'angle formé par l'arc issu de ces vecteurs. On le note . La mesure en radian de l'angle orienté est la mesure en radians de l'arc formé par le couple .
Remarque: sur le dessin, l'angle orienté vaut: 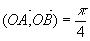
3) Cosinus, sinus dans le cercle trigonométrique
Définition: Soit 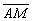 un arc du cercle trigonométrique, alors on peut lire le cosinus de l'angle formé par cet arc sur l'axe horizontal et le sinus sur l'axe vertical (trigonométrie du triangle rectangle). un arc du cercle trigonométrique, alors on peut lire le cosinus de l'angle formé par cet arc sur l'axe horizontal et le sinus sur l'axe vertical (trigonométrie du triangle rectangle).
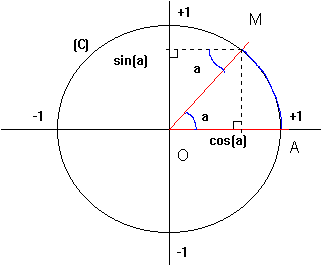
Propriétés:
On voit donc que quel que soit x réel, et et et
De plus on a (théorème de pythagore)
Valeurs remarquables:
| Mesure en rad
|
0
|
|
|
|
|
| Mesure en degré
|
0
|
30°
|
45°
|
60°
|
90°
|
| Sinus
|
0
|
|
|
|
1
|
| Cosinus
|
1
|
|
|
|
0
|
| Tangente
|
0
|
|
1
|
|
Non défini
|
Retour
|
|
|