| Première
|
| Géométrie
|
| Barycentre
|
Barycentre de deux points pondérés
Définition: Soient A, B deux points distincts et a,b deux réels tels que a+b est non nul. Il existe un seul point G tels que 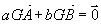 . G est appelé le barycentre des points pondérés A(a) et B(b) . G est appelé le barycentre des points pondérés A(a) et B(b)
Remarque: si a=b=1, alors G est le milieu de [AB]
Propriétés: soit G le barycentre de A(a) et B(b), k un réel non nul alors:
- G est barycentre de A(ka) et B(kb) et
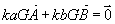
- Les points A, G et B sont alignés et
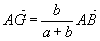
- Soit M un point quelconque, alors
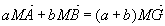
Barycentre de trois points pondérés
Définition: soient A, B et C trois points et a,b et c trois réels tels que a+b+c est non nul, alors il existe un unique point G tel que 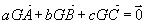 appelé barycentre des points pondérés A(a), B(b) et C(c) appelé barycentre des points pondérés A(a), B(b) et C(c)
Propriétés: soit G le barycentre de A(a), B(b) et C(c), k un réel non nul alors:
Si a=b=c=1 alors G est le centre de gravité du triangle ABC (ou encore isobarycentre)
G est barycentre de A(ka), B(kb), C(kc), et 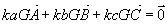
Pour tout point M, 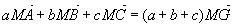
Construction: méthode du barycentre partiel.
Notons H barycentre de A(a) et B(b), alors: 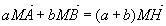 avec M=G on a: avec M=G on a:
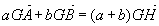 et G barycentre de A(a), B(b) et C(c): et G barycentre de A(a), B(b) et C(c):
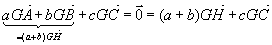 donc G est barycentre de H(a+b) et C(c) donc G est barycentre de H(a+b) et C(c)
Coordonnées de G dans un repère: On prendra O(0,0) l'origine du repère.
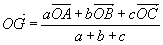 donc donc 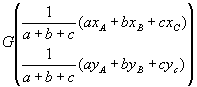
Retour
|
|
|