| Première
|
| Géométrie
|
| Produit scalaire ? lignes de niveaux
|
Produit scalaire
Définitions: Dans un repère (O,i,j) orthonormé, le produit scalaire des vecteurs 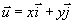 et et 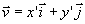 est le réel est le réel 
Si 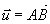 et et 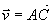 alors: alors:
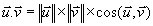
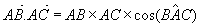
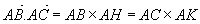
Avec H projeté (orthogonal) de C sur AB et K projeté (orthogonal) de B sur AC:
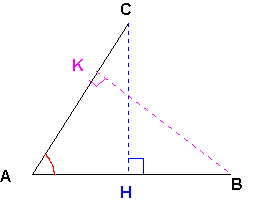
Propriétés:
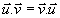
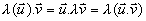
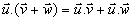
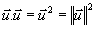
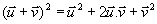 d'où d'où 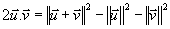
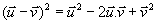 d'où d'où 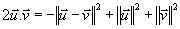
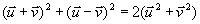
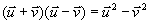
Théorème: 2 vecteurs 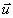 et et 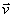 sont orthogonaux si et seulement si sont orthogonaux si et seulement si 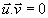
Lignes de niveaux
Définition: soit f une application du plan dans R, on appelle ligne de niveau k de f avec k réel, l'ensemble des points M tels que f(M)=k.
Exemples:
- : l'ensemble E des points M est la droite perpendiculaire à (AB)
- : l'ensemble E des points M est le cercle centré sur I milieu de [AB]
- (avec a+b non num): l'ensemble E des points M est cercle de centre G barycentre de A(a) et B(b)
Retour
|
|
|