| Première
|
| Algèbre
|
| Polynômes et trinômes du second degré
|
Définitions et propriétés
Définition: soit n un entier positif et , ,..., ,... des réels, alors la fonction P:R->R telle que ... est un polynôme de degré n.
Propriétés:
Si pour tout x, P(x)=0, alors P est le polynôme nul, et =...=
Deux polynômes P(x) et Q(x) sont égaux si et seulement s'ils sont de même degré et les coefficients des termes de même degré sont égaux (c'est à dire si et alors pour tout i )
Soit P un polynôme de degré n et b tel que P(b)=0, alors b est une racine du polynôme et P(x)=(x-b)*Q(x) avec Q(x) de degré n-1.
Un polynôme de degré n admet au plus n racines non nulles.
Trinômes et équations du second degré
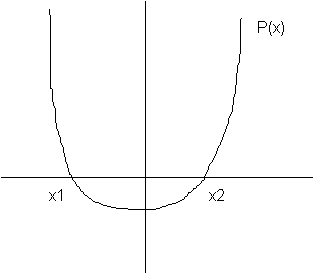
Définition: soit le trinôme du second degré: on s'intéresse à l'équation P(x)=0. La courbe de P(x) est une parabole.
Propriété: deux nombres dont la somme est S et dont le produit est P sont solutions de l'équation
Résolution d'une équation du type :
Posons le discriminant de l'équation. 3 cas se présentent:
est positif:
2 solutions (qui sont les racines du polynôme): 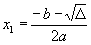 et et 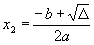
Factorisation:
Signe de P(x): P(x) est du signe de ?a entre les racines et du signe de a en dehors des racines.
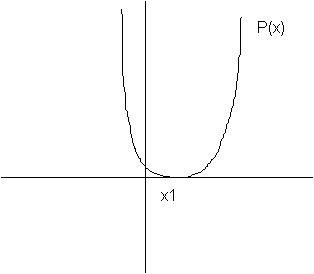
est nul
1 solution double 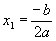
Factorisation:
Signe de P(x): P(x) est du signe de a.
est négatif
Pas de solutions réelles (pour les obtenir voir les complexes)
Pas de factorisation de P(x) possible avec des solutions réelles.
Signe de P(x): P(x) est du signe de a.
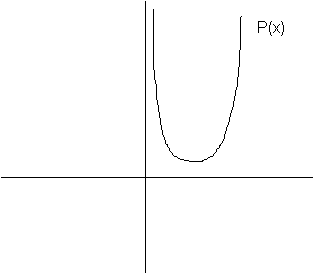
Retour
|
|
|