| Première
|
| Algèbre
|
| Dérivées et calcul différentiel
|
Définitions et première approche
Définition: on appelle nombre dérivé d'une fonction f(x) en un point A(Xa,Ya), le coefficient directeur de la tangente à la courbe Cf au point A (Cf dessin):
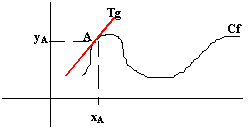
Ce nombre, s'il existe, peut être calculé grâce aux deux formules suivantes:
1/ 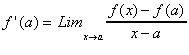
2/ 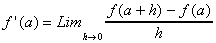
A savoir: si la limite n'existe pas (ou est infinie) alors la fonction n'est pas dérivable au point considéré.
Exemple: soit f(x)=2x-3. Calculer f'(4)
Solutions: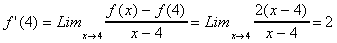 (que l'on retrouve avec les formules). (que l'on retrouve avec les formules).
NB: on a donc l'équation de la tangente en un point A: y=f'(a)(x-a)+f(a)
Définition: une fonction f(x) est dérivable sur un intervalle I si et seulement si elle est dérivable en tout point de I.
NB: En fait le domaine de dérivabilité de f(x) correspond au domaine de définition de sa fonction dérivée.
Dérivées des fonctions usuelles et opérations
Dérivées à connaître et formules utiles:
| Fonctions: f(x)
|
Dérivées f'(x)
|
| a
|
0
|
| x
|
1
|
| ax
|
a
|
| , nR
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ou
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Une astuce: une seule formule très importante à retenir: . En effet, pour u on pose n=1/2 et pour 1/u on pose n=-1. Avec u une fonction quelle qu'elle soit. De même avec n=-a. Essayez donc!!!
Formules de composition et d'opérations de fonctions
Retour
|
|
|