| Première
|
| Algèbre
|
| Les fonctions circulaires
|
Cosinus
Etude de la fonction
Cos est définie sur R et dérivable sur R, la dérivée de la fonction cosinus est cosx'=-sinx
, cosinus est périodique de période deux pi, on étudiera donc la fonction sur l'intervalle . De plus l'étude de la parité nous donne: cos(-x)=cos(x). Cosinus étant paire, on a donc une symétrie par rapport à l'axe Oy.
Le tableau de variation est:
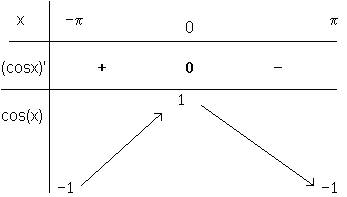
La courbe:
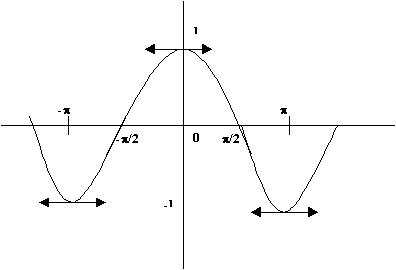
Sinus
Etude de la fonction
Sinx est définie sur R et dérivable sur R, la dérivée de la fonction sinus est sinx'=cosx
, sinus est périodique de période deux pi. On étudiera la fonction sur l'intervalle . De plus, l'étude de la parité nous donne: sin(-x)=-sin(x). Sinus est impaire, on a donc une symétrie par rapport à l'origine du repère, le point 0.
Le tableau de variation est:
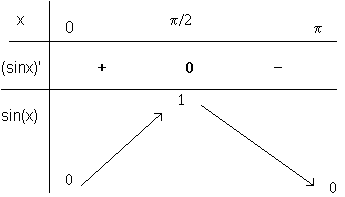
La courbe:
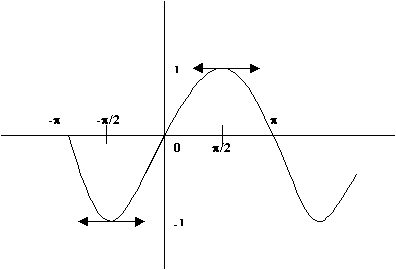
Remarque: la courbe de cosinus est obtenue par une translation de vecteur 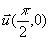 de la courbe de sinus (ou une translation de vecteur de la courbe de sinus (ou une translation de vecteur 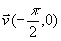 ) )
Tangente
Etude de la fonction
Tan(x)=sin(x)/cos(x) est définie sur D=R\{pi/2+kpi, k entier} et dérivable sur D. La dérivée de la fonction tangente est: .
, tangente est périodique de période pi, on étudiera la fonction sur l'intervalle . De plus l'étude de la parité nous donne tan(-x)=-tan(x). Tangente est impaire, on a donc une symétrie par rapport à l'origine du repère, le point O.
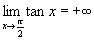
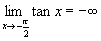
On a donc deux asymptotes verticales d'équation et .
Le tableau de variation est:
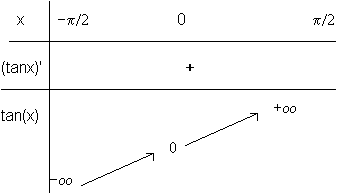
La courbe:
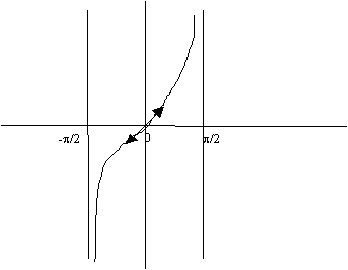
Equations trigonométriques
Du type cosx=cosa:
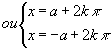 avec k entier. avec k entier.
Cas particulier:
Du type sinx=sina
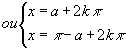 avec k entier avec k entier
Cas particuliers:
NB: pour les équations du type cos(f(x))=cos(a) ou du type sin(f(x))=sin(a), poser u=f(x).
Du type acosx+bsinx=c avec a, b, c des réels et
Poser z=a+ib, alors 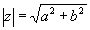 et et 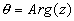 . On a donc: . On a donc:
cos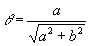 et sin et sin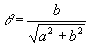
D'où l'expression devient 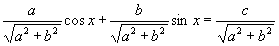
On a des solutions si 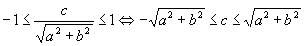
Cas 1: 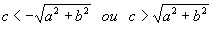 alors S={0} alors S={0}
Cas 2: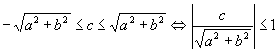 donc il existe d tel que cosd= donc il existe d tel que cosd=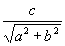 . .
L'équation devient cos(x-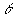 )=cosd avec x= )=cosd avec x=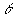 +d+2kpi ou x= +d+2kpi ou x=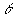 -d+2kpi. -d+2kpi.
Retour
|
|
|