| Classes préparatoires
|
| Algèbre
|
| Les déterminants
|
Définition: soit 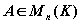 , on définit Det(A) par:
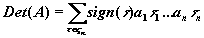
Cette définition est théorique et ne donne pas de calcul.
Théorème: Det(T(A))=Det(A)
Règle de Sarrus: soit la matrice 3x3 suivante  alors le déterminant de celle ci est Det(A)=(ab'c"+a'b"c+a"bc')-(cb'a"+c'b"a+c"ba')
Propriétés des déterminants:
- Si j'échange deux aucune (a,b) Det(A')=-Det(A)
- Même chose si j'échange deux lignes
- Si je multiplie une colonne par k, Det(A')=kDet(A)
- En particulier avec n=nombre de colonnes de A.
- Si je calcule où A1 et A2 ne différent que par une colonne
Conclusion: on dit du déterminant que c'est une application multilinéaire c'est à dire linéaire par rapport à chaque colonne, multilinéaire alternée.
Remarques:
On ne change pas un déterminant en rajoutant à une colonne une combinaison linéaire des autres colonnes.
Le déterminant d'une matrice trigonale est le produit des termes diagonaux.
Boîte à outils: ne pas hésiter à formuler ce que l'on veut faire, ne pas hésiter à encadrer les zones de la matrice où l'on veut effectuer les calculs.
Propriétés:
- Si une matrice a deux lignes identiques, son déterminant est nul.
- Si det(A)=0, A n'est pas inversible.
- Si Det(A) est non nul, C1..CN forment une base de Rn.
- Soit
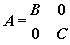 alors det(A)=det(B)*det(C)
- Déterminant d'une matrice trigonale par blocs:
 .
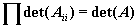Retour
|
|
|