| Classes préparatoires
|
| Algèbre
|
| Applications linéaires particulières
|
I] Les homothéties vectorielles
Définition: on appelle homothétie vectorielle de rapport 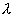
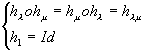 de plus de plus 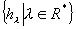 est un sous groupe des automorphismes de groupe GL(E). est un sous groupe des automorphismes de groupe GL(E).
Propriétés
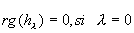
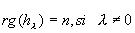
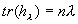
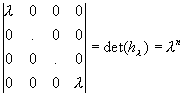
Caractérisation matricielle: c'est 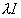 dans toute base. Une homothétie est toujours un endomorphisme symétrique car sa matrice est toujours symétrique dans une base orthonormée. dans toute base. Une homothétie est toujours un endomorphisme symétrique car sa matrice est toujours symétrique dans une base orthonormée.
II] Les projecteurs
Définition: on appelle projecteur 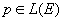 tels que . C'est un élément idempotent (ses puissances, c'est lui même). tels que . C'est un élément idempotent (ses puissances, c'est lui même).
Propriété: x s'écrit x=(x-p(x))+p(x) (tel que (x-p(x)) appartient à Ker(p) et p(x) appartient à Im(p)). C'est la somme d'un vecteur de Ker(p) et d'un vecteur Im(p). Cette décomposition est unique: 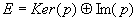
Théorème: si 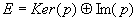 x=x1+x2, x=x1+x2, 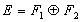 et et 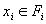 est un projecteur tel que Ker(p)=F1 et Im(p)=F2 et tout projecteur s'obtient ainsi. est un projecteur tel que Ker(p)=F1 et Im(p)=F2 et tout projecteur s'obtient ainsi.
Propriété:
On dit que p est la projection sur F2 parallélement à F1.
Si p est un projecteur: est encore un projecteur.
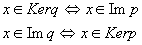
p et q s'appellent des projecteurs supplémentaires: pq=0 et p+q=id.
Projecteurs triviaux:
alors kerp=0 et Imp=E
alors kerp=E et Imp=0
Les autres projecteurs sont appelés projecteurs vrais.
Matrice d'un projecteur 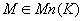 et et
Dans une base adaptée à la DSD 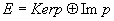 : :
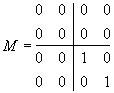 , Det(p)=0 si ce n'est pas Id et Tr(p)=dim(Imp)=rg(p) , Det(p)=0 si ce n'est pas Id et Tr(p)=dim(Imp)=rg(p)
Un projecteur n'est jamais une application orthogonale.
III] Les symétriques
Rappel: 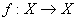 est involutive si et seulement si fof=Id. On dit que c'est une involution. est involutive si et seulement si fof=Id. On dit que c'est une involution.
Définition: on appelle symétrie de E 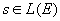 qui est involutive. S est une symétrie si et seulement si et qui est involutive. S est une symétrie si et seulement si et 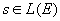
Retour
|
|
|