| Classes préparatoires
|
| Géométrie
|
| Cercles sphères
|
I] Le cercle dans le plan E: dim E = 2, euclidien, affine
Définition: le cercle de centre I de rayon R est l'ensemble 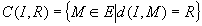
Théorèmes:
L'équation dans R du cercle de centre I(a,b) de rayon R est
L'équation de sa tangente en (x0,y0) est
Il a pour équation paramétrée: 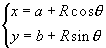
Avec 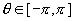 ou ou 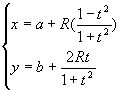 et et 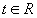
Réciproquement, l'équation représente:
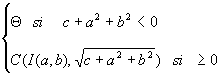
Intersection avec une droite: D une droite et C(I,R) avec R>0:
- Si d(I,D)>R,
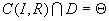
- Si d(I,D)=R,
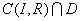 =1 point, projection orthogonale de I sur D. =1 point, projection orthogonale de I sur D.
- Si d(I,D)<R,
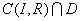 =2 points distincts. =2 points distincts.
Intersection de deux cercles: deux cercles C1(I1,R1) et C2(I2,R2) avec R1R2>0.
- Si d(I1,I2)>R1+R2 où d(I1,I2)<|R1-R2| alors
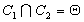
- Si |R1-R2|<d(I1,I2)<R1+R2 alors
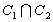 =2 point distincts. =2 point distincts.
- Si d(I1,I2)=R1+R2 où d(I1,I2)=|R1-R2| alors
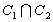 =1 point. =1 point.
Soient 2 points A, B alors l'ensemble des points M tels que AM=kBM est un cercle centré sur la droite AB.
Soient 2 points A et B distincts, 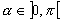 , l'ensemble des points M tels que , l'ensemble des points M tels que 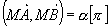 est un cercle passant par A et B privé des points A et B. Pour est un cercle passant par A et B privé des points A et B. Pour 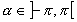 c'est un arc de cercle d'extrémité A et B avec c'est un arc de cercle d'extrémité A et B avec 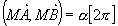
Définition: on a 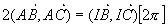 avec A, B, C trois points distincts du cercle. avec A, B, C trois points distincts du cercle.
II] Cercle et sphère dans l'espace
Définition: Dans la sphère de centre I de rayon R est 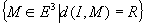 . .
Théorème: l'équation d'une sphère S de centre I(a,b,c) de rayon R est (dans un RON):
ou
Si alors
Si alors
Théorème: l'intersection de S(I,R) et du plan P est:
Vide si d(I,P)>R
Projection orthogonale de I sur P si d(I,P)=R
Cercle de P centré sur I'=projection de I sur P et de rayon sinon.
Théorème: le plan tangent en M0(x0,y0,z0) à la sphère S(I,R), R>0 d'équation où a pour équation:
c'est le plan passant par M0 et orthogonal à Im0.
Théorème: soient deux sphères S(I,R) et S'(I',R') avec R, R' >0 alors:
Si d(I,I')>R+R' ou d'(I,I')<|R-R'| => 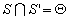
Si 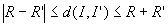 alors alors 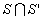 est un cercle ou un point quand d(I,I')=R+R'. est un cercle ou un point quand d(I,I')=R+R'.
III] Equations paramétrées
Cercle: 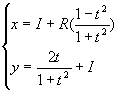 en polaire: en polaire: 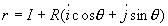
Sphère: 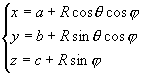 avec avec 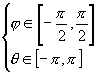
Equation en polaires:
Cercle: de centre O, r=cste
Passant par O centre 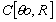 alors alors 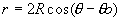
Droite passant par O: 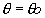
Autres: 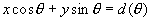 équation d'Euler avec équation d'Euler avec 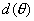 distance OH (distance de O à la droite) distance OH (distance de O à la droite)
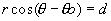
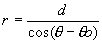 avec avec 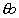 = angle = angle 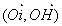
Retour
|
|
|