| Classes préparatoires
|
| Analyse
|
| Equations différentielles du premier ordre
|
I] Equations linéaires du premier ordre du type y'=a(t)y+b(t)
Equation homogène: y'=a(t)y
Soit 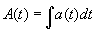 alors alors 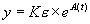 avec avec 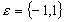 (c'est le signe de y). (c'est le signe de y).
On prend les solutions sur les intervalles In où a(t) ne s'annule pas.
Solution particulière: y'-a(t)y=b(t)
Si b(t) est un polynôme, chercher une solution polynomiale (de même degré avec a(t)=constante)
Si 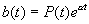 alors la solution est de la forme alors la solution est de la forme 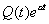 où Q(t) est un polynôme de même degré. où Q(t) est un polynôme de même degré.
Faire varier la constante 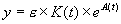
Solution complète
C' est la somme de la solution particulière et des solutions de l'équation homogène.
Conditions de raccordement
Si on a deux solutions L1 sur I1 et L2 sur I2 on doit avoir:
Lim L1= Lim L2 (au point où a(t) s'annule)
Lim L'1=Lim L'2
II] Equations géométriques: équations différentielles ordinaires homogènes du type x+y'F(y,x)=0 (exemple: x+(y-2x)y'=0)
Si en posant 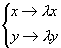 y' reste inchangée, alors l'équation est homogène. y' reste inchangée, alors l'équation est homogène.
On cherche les solutions du type y=mx.
On cherche les solutions du type 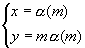 on a une équation linéaire on a une équation linéaire 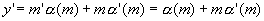 . .
Les solutions sont donc sous forme paramétriques.
III] Equations à variables séparées de la forme a(x)=y'b(y)
Mettre sous la forme a(x)dx=b(y)dy et alors 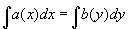 d'où A(x)+K=B(y) d'où A(x)+K=B(y)
IV] Equations de Bernouilli y'=a(x)y+b(x)y^c
Poser z=1/y^(c-1) on a alors une équations linéaire:
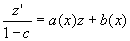
VI] Equations de Lagrange et Clairaut y=xa(y')+b(y') ou y=xy'+b(y')
Poser y'=t=dy/dx donc dy=tdx et y=xa(t)+b(t)
D'où tdx=dy=a'(t)xdt+a(t)dx+b'(t)dt
On obtient x(t) par : tdx=a'(x)dt+a(t)dx+b'(t)dt
[t-a(t)]dx=[a'(t)xb'(t)]dt
et x'=dx/dt=(a'(t)x+b'(t))/(t-a(t)) c'est une équation différentielle linéaire.
Il suffit de résoudre y=xa(t)+b(t)
On a des solutions sous forme paramétrique.
Retour
|
|
|