| Classes préparatoires
|
| Analyse
|
| Equations différentielles du second ordre
|
I] Equations différentielle à coefficient constants
Equation homogène: y''+ay'+by=0
Equation caractéristique
, deux racines 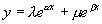 , avec , avec 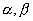 solutions. solutions.
, une racine double: 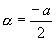 et et 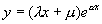
, deux racines complexes conjuguées, 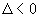 et et 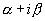
Solution particulière
Le second membre est un polynôme: y''+ay'+by=P(t), P(t) de degré n.
Si b est non nul, la solution est un polynôme de degré n.
Si b est nul et a non nul, la solution est un polynôme de degré n+1.
Si b et a sont nuls, la solution est un polynôme de degré n+2.
Le second membre est : 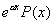 , on pose , on pose
Si k non racine de E: solution du type 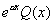 avec Q du même degré que P. avec Q du même degré que P.
Si k racine simple de E: solutions du type 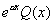 avec Q de degré n+1. avec Q de degré n+1.
Si k racine double de E: solutions du type 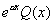 avec Q de degré n+2. avec Q de degré n+2.
Le second membre est: A(x)cos(cx)+B(x)sin(cx)
Si ax non racine de e: solution du type 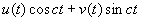 avec avec 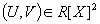
Et sup(d°U,d°V)=1+sup(d°A,d°B)
Le second membre est 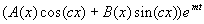 , poser , poser 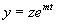
Variation de la constante: y''+ay'+by=d(t)
Si E: 2 racines: 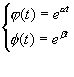
Racine double: 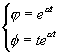
2 racines complexes: 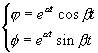
On a une base 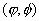 , on cherche une solution telle que: , on cherche une solution telle que:
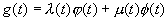 et et 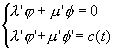 , on obtient alors toutes les solutions. , on obtient alors toutes les solutions.
Retour
|
|
|