| Classes préparatoires
|
Analyse
Une petite théorie du rang
|
| |
I] Définitions
Définitions
- Soit un système de vecteurs V1,V2,...,VN, on appelle rang de ce système dim Vect(V1,V2,...,Vn).
- Soit f:E->F une application linéaire, on appelle rang de f la dim(imf)=rg(f).
- Soit M une matrice
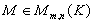 elle définit (aux bases près) elle définit (aux bases près) 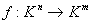
Alors rg(M)=rg(f).
Remarque: Si M et N sont équivalentes, rg(M)=rg(N)
Soit n le nombre de colonnes de M, alors 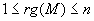
Le rang d'un système de vecteurs n'est rien d'autre que le nombre maximal de vecteurs indépendants que l'on peut extraire: 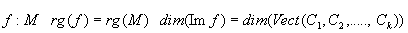
Le rang d'une matrice M n'est rien d'autre que le nombre maximal de colonnes indépendantes de M.
Théorème du rang: soit 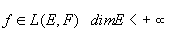 alors rg(f)+dim(kerf)=dim(E) et alors rg(f)+dim(kerf)=dim(E) et 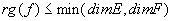
Si 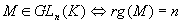
Cas particuliers: les matrices de rang 1: il y au moins une colonne distincte de 0 (par exemple Cj). Soit Ck avec k différent de J. Si rg M =1, 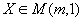 et et 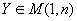 et et 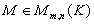 alors M=XY. alors M=XY.
Matrice de rang 1: une colonne non nulle, les autres sont des multiples de celle là.
Rg(t(M))=Rg(M)
II] Matrices semblables
Définition: M et M' sont semblables si et seulement si où 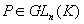 . Semblables = de même rang. . Semblables = de même rang.
Trace: tr(AB)=tr(BA)
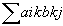 et tr(AB)= et tr(AB)=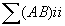
Conclusion: trace de : . Deux matrices semblables ont même trace.
Déterminant: Det(AB)=Det(A)Det(B) et .
Retour
|
|
|