| Classes préparatoires
|
| Analyse
|
| Suite et série de fonctions
|
I] Suites de fonctions
Définitions
Une suite de fonctions est une application de N vers N.
Fn converge simplement vers f si et seulement si 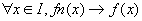
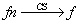 sur I, sur I, 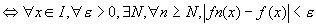
 sur I, sur I, 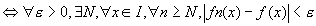
Méthode pour l'étude:
- Si pas de CS alors c'est terminé.
- Si on peut trouver une suite
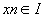 telle que fn(xn)-f(xn) ne converge pas vers 0, alors pas de CVU. telle que fn(xn)-f(xn) ne converge pas vers 0, alors pas de CVU.
- Sinon on étudie
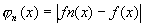 et on cherche et on cherche 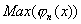 . Si . Si 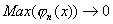 alors gagné. alors gagné.
Propriétés de la convergence uniforme
Théorèmes:
- Fn définies sur I, si
 et fn continues, alors f continue. et fn continues, alors f continue.
- Fn définies sur I=[a,b], si
 et fn continues alors en posant et fn continues alors en posant 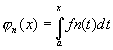 et et 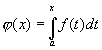 , on a , on a 
- Fn définies sur I et
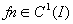 si si 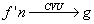 , si , si 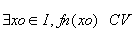 alors alors  et f'=g. et f'=g.
Propriété: 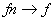 , suite CVS définies sur I. S'il existe une suite Un convergeant vers 0 telle que : , suite CVS définies sur I. S'il existe une suite Un convergeant vers 0 telle que : 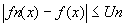 alors il y a CVU. alors il y a CVU.
II] Séries de fonctions
Définitions
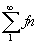 : posons : posons 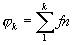 : c'est une somme de fonctions: si : c'est une somme de fonctions: si 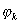 a une limite f, c'est: a une limite f, c'est: 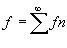
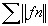 CV CV 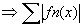 CV CV 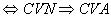 (cv normale implique cv absolue) et (cv normale implique cv absolue) et 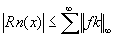
Théorèmes
- Si on a CVN, on a CVA et donc CVU.
- Si les fn sont continues, la série CVU, alors la somme de la série est continue.
- Fn continues sur [a,b],
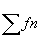 CVU on a CVU on a 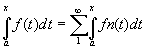 d'où d'où 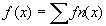
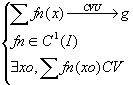 alors alors 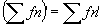 en particulier si CVN. en particulier si CVN.
Retour
|
|
|