| Classes préparatoires
|
| Analyse
|
| Suites réelles
|
Définition: Un converge 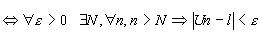
Propriétés
- Toute suite convergente est bornée.
- Un bornée,
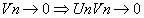
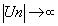 et minorée, et minorée, 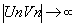
Théorème d'encadrement:
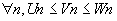 alors alors 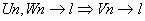
Si alors 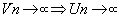
Relations de comparaison
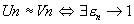 telle que telle que 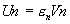 équivalentes. équivalentes.
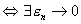 telle que telle que 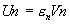 négligeables. négligeables.
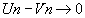
et sont asymptotiques.
Propriétés
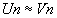 si si 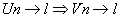
, 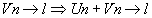
Suites de références
- a>1,
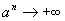
- a=1,
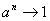
- a=1, suite divergente bornée.
- a<1, suite divergente non bornée
Critère de d'Alembert pour les suites
1 Un une suite, si 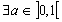 tel que tel que 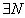 tel que tel que 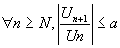 alors alors 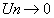
2 Si a>1, N tel que 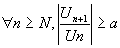 alors alors 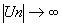
Résumé de comparaison
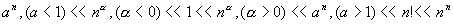
Convergence
Un croissante majorée converge vers
Un décroissante minorée converge vers
Suites adjacentes
et sont adjacentes si An est croissante, Bn est décroissante et 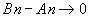
Propriété: deux suites adjacentes sont convergentes et ont même limites.
Suites extraites
Toute suite extraite 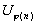 de où de où 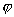 est croissante de N dans N alors est croissante de N dans N alors 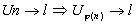
Suite de Cauchy:
est de Cauchy si t seulement si 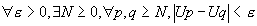 dans un espace complet ou de Banach, toute suite de Cauchy est convergente. dans un espace complet ou de Banach, toute suite de Cauchy est convergente.
Théorème de composition des limites:
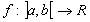 admet une limite admet une limite 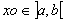
Si alors à partir d'un certain rang, existe et
Suite tendant vers 0 : 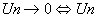 est bornée et est bornée et 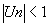 pour pour 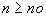
Suite du type
Propriétés
- converge si et seulement si
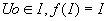 (I stable par f, f croissante et Lim Un=(l)=l vrai si f est continue) (I stable par f, f croissante et Lim Un=(l)=l vrai si f est continue)
- croissante si et seulement si
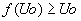
- décroissante si et seulement si
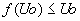
- Si f est décroissante sur I,
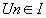 , alors est monotone. , alors est monotone.
- Si f est décroissante sur I,
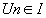 , et sont monotones et varient en sens contraire. , et sont monotones et varient en sens contraire.
Méthode
- Etudier f, solutions de f(x)=x et le signe de f(x)-x
- Chercher les intervalles stables par f
- Faire une étude en fonction de
Théorème du point fixe:
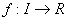 application contractante (K lipschitzienne) si et seulement si application contractante (K lipschitzienne) si et seulement si 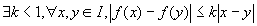
Si f est contractante, alors est de Cauchy et converge.
Sens de Cesaro: Si 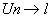 alors alors 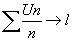
Suites complexes:
Convergence: converge 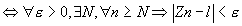 c'est à dire c'est à dire 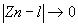
Propriétés
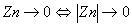
Si 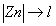 et et 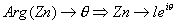
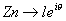 alors alors 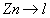
Si et l=x+iy alors 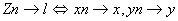
Méthode
On étudie les deux suites et .
On étudie les deux suites et
Astuces
Faire le tour des évidences: supérieure ou égale à 0, croissante, supérieure ou égale à 1.
Connaître les astuces de calcul:
- Ajouter et enlever un nombre
- Multiplier et diviser par le même nombre.
- Si on connaître la limite 1 de la suite, étudier .
Retour
|
|
|