| Classes préparatoires
|
| Analyse
|
| Suites spécifiques
|
I] Suites récurrentes linéaires d'ordre deux du type Un+2=aUn+1+bUn
Equation caractéristique: avec r non nul.
On a deux racines, 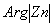
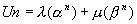 et et 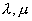 sont déterminés par les deux premiers termes de la suite: sont déterminés par les deux premiers termes de la suite:
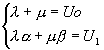
Remarque: si l'équation caractéristique a une racine double, les suites sont 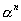 et et 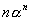 au lieu de au lieu de 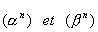 et alors: et alors:
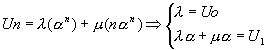
Suites récurrentes affines du types
Si b=0 on a une suite arithmético géométrique
1/ Si a+b=1 et a différent de 2 alors on pose 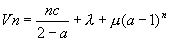
2/ Si a=2, b=-1 alors on pose 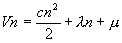
1/ donne les racines de l'équation caractéristique sont 1 et ?b=a-1 donc les racines sont différentes et les suites sont du type 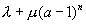
2/ donne l'équation caractéristique qui admet 1 pour racine double. Les suites sont donc 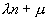
II] Les suites arithmético géométriques
Arithmétiques
donc
Somme: 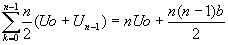
converge si et seulement si b=0
Géométriques
donc
Somme: 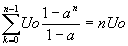 si a=1 si a=1
Un converge si et seulement si 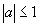 , si , si 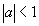 alors et alors et 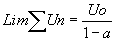
Arithmético géométriques:
si a est différent de 1 on pose 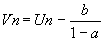 et est géométrique de raison a. et est géométrique de raison a.
On pose 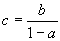 et et 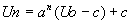
III] Suites homographiques
Du type 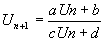 avec avec 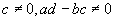
On pose 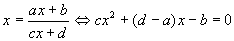
- Soit
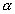 une racine de l'équation. Si une racine de l'équation. Si 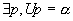 alors Un et constante. alors Un et constante.
- Si
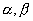 deux racines de l'équation: on pose deux racines de l'équation: on pose 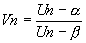 , c'est une suite géométrique et , c'est une suite géométrique et 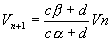
- Si une racine double
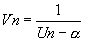 c'est une suite géométrique et c'est une suite géométrique et 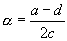
- On a
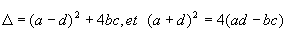 et et 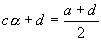 , , 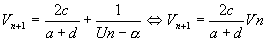 et Vn définie pour tout et Vn définie pour tout 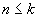 tel que tel que 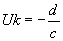
- Si deux racines distinctes et
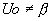 on pose on pose 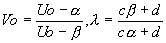 . Il faut que . Il faut que 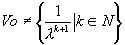
- Si une racine double et
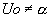 . On pose . On pose 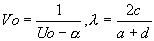 , il faut que , il faut que 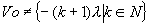 . .
Retour
|
|
|