| Travaux numériques
|
| 09. Equations, inéquations à une inconnue, systèmes
|
02. Inéquations, systèmes d'inéquations à une inconnue
Exercice 1
|
Inéquations mode d'emploi
 L'équation à une inconnue x n'a qu'une solution, le nombre 2. Le nombre 2 est donc la seule valeur de x pour laquelle les deux expressions et sont égales. L'équation à une inconnue x n'a qu'une solution, le nombre 2. Le nombre 2 est donc la seule valeur de x pour laquelle les deux expressions et sont égales.
Si on remplace x dans l'équation par un autre nombre que 2 alors les deux expressions sont inégales (différentes) ce qui s'écrit:.
Quand deux nombres sont différents, il y en a toujours un qui est plus grand que l'autre donc on a obligatoirement ou .
On vient d'écrire des inégalités à une inconnue x, donc des inéquations. Le symbole > qui se lit de gauche à droite "strictement supérieur à" s'appelle le sens de l'inégalité.
 Puisque l'équation a une seule solution 2, les deux inéquations et ont pour solutions tous les autres nombres réels. Puisque l'équation a une seule solution 2, les deux inéquations et ont pour solutions tous les autres nombres réels.
Comme on l'a vu pour l'équation , si on veut trouver les solutions de l'inéquation , il faut la transformer.
Il existe deux transformations permettant de transformer une inéquation en une inéquation de mêmes solutions.
Transformation 1: On peut, sans changer les solutions, ajouter un même nombre aux deux membres d'une inéquation.
Cette transformation est la même que pour une équation, donc les conventions de langage sont les mêmes.
Transformation 2: On peut, sans changer les solutions, multiplier ou diviser par un même nombre non nul les deux membres d'une inéquation. De plus:
- si le nombre est strictement positif, on conserve le sens de l'inégalité,
si le nombre est strictement négatif, on change le sens de l'inégalité.
La transformation 2 diffère de celle donnée pour une équation. La différence réside dans le fait qu'il faut connaître le signe du nombre par lequel on multiplie ou divise et, suivant celui-ci, conserver ou changer le sens de l'inégalité.
 Résolution de l'inéquation d'inconnue x. Résolution de l'inéquation d'inconnue x.
|
Commentaire |
|
On fait passer x au premier membre et 3 au second. |
|
On a réduit les deux membres. |
| On divise les deux membres par qui est strictement . |
On veut obtenir x dans le premier membre. Le seul moyen c'est de diviser par 3. |
|
|
On divise le premier membre et le deuxième par 3, puis on écrit le sens (le même que le précédent puisque 3 est strictement positif). |
| Les solutions de l'inéquation sont visiblement tous les nombres strictement à . |
L'inéquation a une infinité de solutions que l'on ne peut énumérer. C'est une différence importante par rapport aux équations qui ont en général un nombre fini de solutions.
Les nombes solutions sont représentés sur la demi-droite graduée d'origine O par tous les points de la demi-droite ]Ax).
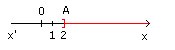 |
 Résolution de l'inéquation d'inconnue x. Résolution de l'inéquation d'inconnue x.
|
Commentaire |
|
On fait passer au second membre et 3 au premier. |
|
On a réduit les deux membres. |
| On divise les deux membres par qui est strictement . |
On veut obtenir x dans le premier membre. Le seul moyen c'est de diviser par -3. |
|
|
On divise le premier membre et le deuxième par -3, puis on écrit le sens, le sens contraire du précédent, puisque -3 est strictement négatif. |
| Les solutions de l'inéquation sont visiblement tous les nombres strictement à . |
Il suffit de lire l'inégalité:"x inférieur strictement à 2". |
Les solutions de l'équation et des deux inéquations et sont représentées sur le schéma ci-dessous:
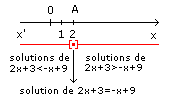
Retour
|
|
|