| Travaux numériques
|
| 09. Equations, inéquations à une inconnue, systèmes
|
02. Inéquations, systèmes d'inéquations à une inconnue
Exercice 3
|
Résoudre une inéquation du premier degré
Inéquation 1
On développe le second membre.
1.
On rassemble les termes en x au premier membre et les termes constants au second.
2.
3.
On divise les deux membres par , qui est strictement .
4.
5.
Les solutions de l'inéquation sont tous les nombres strictement à .
Commentaire
Ligne 4. On conserve le sens de l'inéquation parce que 8 est de signe plus.
Sur le schéma, les solutions de l'inéquation sont représentées par tous les points de la demi-droite (x'A[.
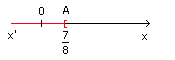 |
| ____________________________________________________________________________________________________________________ |
Inéquation 2
On développe le premier membre.
1.
On rassemble les termes en x au premier membre et les termes constants au second.
2.
3.
On divise les deux membres par , qui est strictement .
4.
5.
Les solutions de l'inéquation sont tous les nombres (trois mots) à .
Commentaire
Le symbole se lit "inférieur ou égal à". Les solutions de l'inéquation sont tous les nombres solutions de l'inéquation et le nombre solution de l'équation .
Ligne 4. On change le sens de l'inéquation parce que -3 est de signe moins.
L'inéquation a une infinité de solutions, la plus grande de toutes est . Il n'existe pas de plus petite solution.
Sur le schéma, les solutions de l'inéquation sont représentées par tous les points de la demi-droite (x'A[.
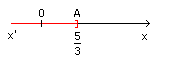 |
| ____________________________________________________________________________________________________________________ |
Inéquation 3
1.
On rassemble les termes en x au premier membre et les termes constants au second.
2.
3.
Pour toute valeur de x l'inégalité obtenue est . Elle est , donc l'inéquation (quatre mots).
Commentaire
Ligne 2. Les termes en x s'annulent.
Ligne 3. On obtient une inégalité numérique fausse. |
| ____________________________________________________________________________________________________________________ |
Inéquation 4
On multiplie les deux membres par , qui est strictement .
1.
On développe les deux membres.
2.
On rassemble les termes en x au premier membre et les termes constants au second.
2.
3.
On divise les deux membres par , qui est strictement .
4.
5.
Les solutions de l'inéquation sont tous les nombres strictement à .
Commentaire
Il existe deux dénominateurs 5 et 2. Pour qu'il n'y ait plus de dénominateur, il faut multiplier les deux membres par leur produit .
Ligne 4. On conserve le sens de l'inéquation parce que 14 est de signe plus.
Sur le schéma, les solutions de l'inéquation sont représentées par tous les points de la demi-droite ]Ax).
 |
| ____________________________________________________________________________________________________________________ |
Inéquation 5
On développe le premier membre.
1.
On rassemble les termes en x au premier membre et les termes constants au second.
2.
Pour toute valeur de x l'inégalité obtenue est . Elle est , donc l'inéquation a pour solutions tous les nombres.
Commentaire
Les solutions sont représentées par tous les points de la droite graduée. |
 Méthode Méthode
Pour résoudre une inéquation du premier degré en x, on rassemble les termes en x au premier membre et les termes constants dans l'autre. Si le coefficient a de x est différent de 0, alors on divise les deux membres de l'inéquation par celui-ci, en gardant le sens de l'inéquation si , en le changeant si .
Si le coefficient de x est nul, alors l'inéquation a pour solutions tous les nombres réels ou n'a pas de solution, suivant que l'inégalité obtenue est vraie ou fausse.
Retour
|
|
|