| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 3 (enseignement obligatoire)
|
Enoncé.
Dans chacun des cas ci-dessous, on donne trois fonctions et la représentation graphique C de l'une d'entre elles.
Retrouver celle qui est représentée, en expliquant, à partir des propriétés des fonctions, ce qui vous permet d'éliminer chacune des deux autres.
Premier cas
; ;
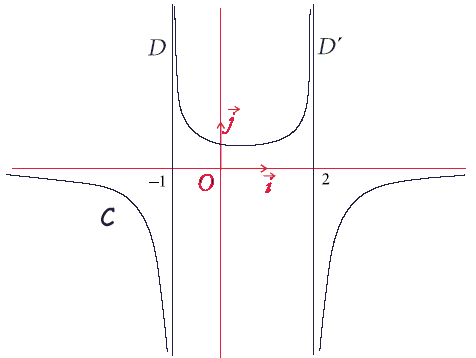
Deuxième cas
; ;
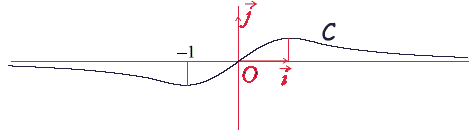
Troisième cas
; ;
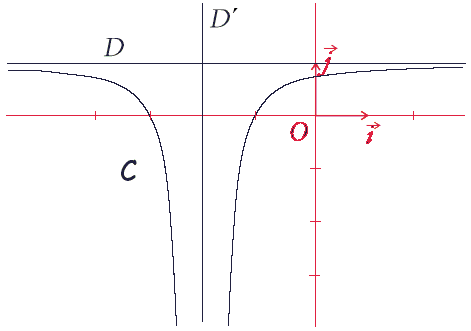
Solution
Premier cas

est définie pour tous les réels x tels que , donc pour tous réels x différents de 1 et de ?2.
C a visiblement pour asymptotes les droites d'équations et , ce qui signifie que la fonction qu'elle représente n'est pas définie pour les valeurs ?1 et 2 de x. Donc la courbe C ne représente pas la fonction .
, donc sa courbe représentative passe par le point de coordonnées .
Le point de C d'abscisse 0 a visiblement une ordonnée positive. Donc la courbe C ne représente pas la fonction .
On en déduit que C représente la fonction .
Deuxième cas

, donc sa courbe représentative passe par le point de coordonnées .
Le point de C d'abscisse 0 est visiblement le point O d'ordonnée 0. Donc la courbe C ne représente pas la fonction .
à 0.1 près, donc sa courbe représentative passe par le point de coordonnées .
Le point de C d'abscisse ?1 a visiblement une ordonnée comprise entre ?1 et 0. Donc la courbe C ne représente pas la fonction .
On en déduit que C représente la fonction .
Troisième cas

à 0.1 prés, donc sa courbe représentative passe par le point de coordonnées .
Le point de C d'abscisse 0 a visiblement une ordonnée strictement inférieure à 1. Donc la courbe C ne représente pas la fonction .
, donc sa courbe représentative passe par le point de coordonnées .
Le point de C d'abscisse 0 a visiblement une ordonnée strictement supérieure à 0. Donc la courbe C ne représente pas la fonction .
On en déduit que C représente la fonction .
Retour
|
|
|