| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 4 (enseignement obligatoire)
|
Enoncé
Pour chacune des deux questions suivantes, indépendantes l'une de l'autre, il vous est proposé plusieurs affirmations. Répondre par OUI ou NON à chaque affirmation en cochant la case qui convient.
Notation: une bonne réponse rapporte un point, une mauvaise réponse en retire un; la note finale par question ne peut être inférieure à zéro.
Question 1
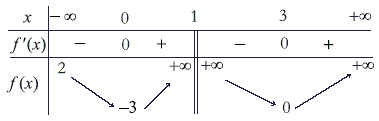
On a donné ci-dessus le tableau de variation d'une fonction f définie et dérivable sur . On appelle sa représentation graphique dans le repère .
On peut alors affirmer que:
| |
OUI |
NON |
| La droite d'équation est asymptote à la courbe . |
|
|
| La droite d'équation est asymptote à la courbe . |
|
|
| La droite d'équation coupe la courbe exactement en deux points. |
|
|
Question 2
Soit g une fonction dérivable et strictement croissante sur .
On peut alors affirmer que:
| |
OUI |
NON |
| . |
|
|
| Pour tout x de , |
|
|
Solution
Question 1
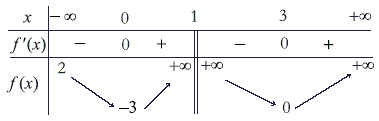
 La droite d'équation est asymptote à la courbe .
Réponse: Non
Explication: f est définie pour la valeur 2,donc ne peut avoir pour asymptote cette droite.
La droite d'équation est asymptote à la courbe .
Réponse: Oui
Explication: La limite de f en 1 est égale à .
La droite d'équation coupe la courbe exactement en deux points.
Réponse: Non
Explication:
La fonction f est strictement monotone et dérivable, donc continue sur les intervalles , et et 3 appartient aux intervalles et , donc l'équation a une solution unique dans chaque intervalle, ce qui fait exactement trois solutions. On en déduit que la droite d'équation coupe la courbe exactement en trois points.
Question 2
Soit g une fonction dérivable et strictement croissante sur .
On peut alors affirmer que:
.
Réponse: Non
Explication:
Le tableau de variation de g est le suivant:
Celui-ci ne permet pas de savoir si la limite de g en existe et si oui, quelle est sa valeur, sauf qu'elle ne peut pas être égale à .
Pour tout x de , .
Réponse: Oui
Explication:
La fonction g est strictement croissante sur , donc pour tout x de
.
Retour
|
|
|