| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 5 (enseignement obligatoire)
|
Enoncé
Soit f une fonction définie et dérivable sur l'intervalle . La courbe représentative C de la fonction dérivée f ' de la fonction f est tracée ci-dessous dans un repère orthogonal .
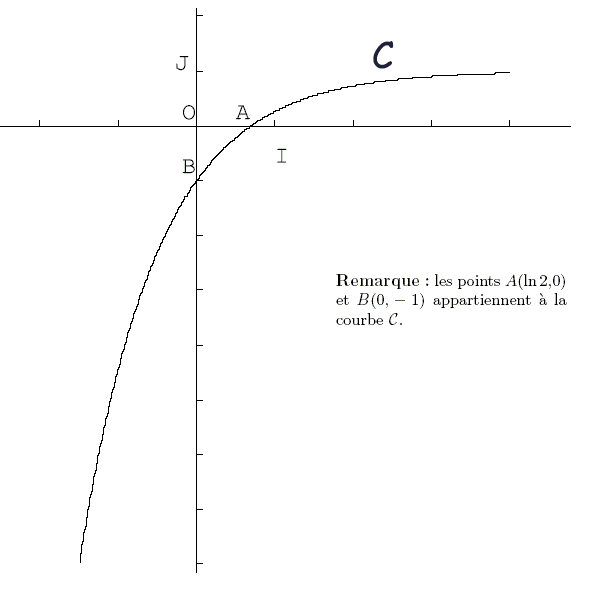
1- Donner le sens de variation de f sur son ensemble de définition. Justifier la réponse.
La représentation graphique de f est appelée .
2- Déterminer le coefficient directeur de la tangente à au point d'abscisse 0.
3- Dans cette question on suppose que .
Dire, pour chacune des affirmations suivantes, en justifiant la réponse donnée, si elle est vraie, fausse ou si le texte ne permet pas de répondre:
a) la droite d'équation est tangente à .
b) L'équation n'a pas de solution dans l'intervalle .
Solution
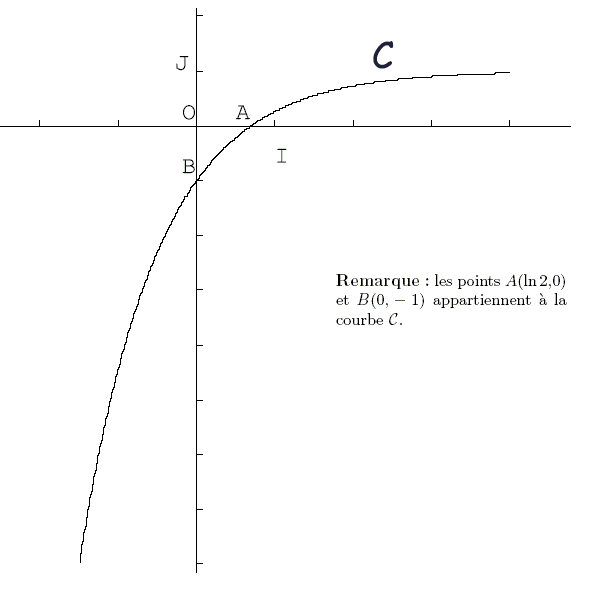
1- C est au-dessous de l'axe des abscisses pour tout réel de , donc , donc f est strictement décroissante sur .
C est au-dessus de l'axe des abscisses pour tout réel de , donc , donc f est strictement croissante sur .
On en déduit le tableau de variation de f:
2- Puisque le point B a pour coordonnées , alors , donc le coefficient directeur de la tangente à la courbe au point d'abscisse 0 est ?1.
3- a) Réponse: L'affirmation est vraie.
Justification: Puisque et , alors la tangente au point d'abscisse et d'ordonnée 1 a pour coefficient directeur 0 , donc pour équation c'est-à-dire .
b) Réponse: L'affirmation est vraie.
Justification: Pour tout x de l'intervalle, , donc il n'existe pas de valeur de x telle que , donc l'équation n'a pas de solution dans .
Retour
|
|
|