| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 9 (enseignement de spécialité)
|
Enoncé
La courbe ci-dessous est une partie de la courbe représentative de la fonction qui à x associe dans un repère orthonormal.
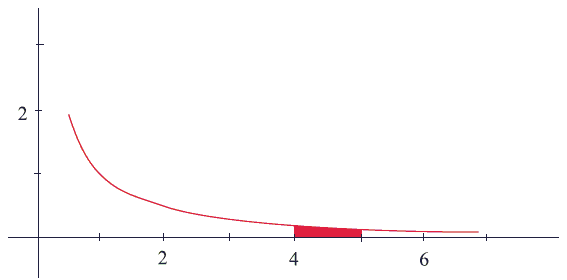
1- Déterminer la valeur exacte de l'aire du domaine hachuré.
2- Soit n un entier naturel strictement positif. On considère l'aire du domaine situé entre les droites d'équations ,, l'axe des abscisses et la courbe C.
a) Montrer que .
b) Quelle est la limite de la suite ?
3- On pose la somme de tous les termes de la suite de à .
a) Déterminer un domaine plan dont l'aire est égale à .
b) Exprimer en fonction de n.
c) Quelle est la limite de la suite ?
Solution
1- L'aire du domaine hachuré est en unités d'aire .
Une primitive sur de la fonction qui à x associe est la fonction logarithme népérien, donc .
2- a)
b) , donc
3- a) est l'aire du domaine situé entre les droites d'équations et , l'axe des abscisses et la courbe C.
b) c)
Retour
|
|
|