| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 11 (enseignement obligatoire)
|
Enoncé
Préambule
Le plan est muni du repère orthonormal (unité graphique: 2 cm).
est la droite d'équation et D est la droite d'équation .
f est une fonction définie et continue sur l'ensemble ;
F est une primitive de f sur ;
C désigne la courbe représentative de la fonction f;
désigne la courbe représentative de la fonction F;
On donne les cinq informations suivantes:
 ;
Le point A(1,3) appartient à ;
;
D est asymptote à en ;
F est strictement croissante sur et strictement décroissante sur .
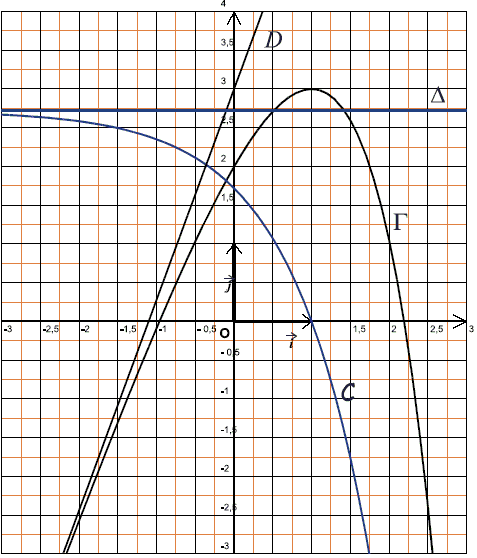
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Déterminer si les affirmations suivantes sont vraies. Justifier vos réponses à l'aide des cinq informations données en préambule:
1- est asymptote à C en .
2- f est positive ou nulle sur et négative ou nulle sur .
3- L'aire de la région du plan comprise entre la courbe C et les droites d'équations , et est égale à 4 centimètres carrés.
Partie B
Un élève affirme avoir trouvé deux fonctions pouvant correspondre aux fonctions f et F présentées en préambule.
Ce sont les fonctions g et h définies sur par et .
1- Quelle est celle qui est susceptible de correspondre à la fonction F? Justifier.
2- Vérifier qu'il n'y a pas de contradiction avec les cinq informations énoncées en préambule.
Le graphique fourni en préambule peut permettre d'illustrer les justifications proposées.
Solution
Partie A
1- , donc l'affirmation: est asymptote à C en est vraie.
2- F est strictement croissante sur et strictement décroissante sur et f est la dérivée de F, donc l'affirmation: f est positive ou nulle sur et négative ou nulle sur est vraie.
3- L'aire, en unités d'aire, de la région du plan comprise entre la courbe C et les droites d'équations , et est égale à .
F est une primitive de f sur , donc .
Le point A(1,3) appartient à , donc et de plus .
On en déduit:
Le plan est muni du repère orthonormal (unité graphique: 2 cm), donc une unité d'aire vaut centimètres carrés.
L'aire de la région du plan comprise entre la courbe C et les droites d'équations , et est donc égale à , donc 4 centimètres carrés.
L'affirmation est vraie.
Partie B
1- et .
Puisque , alors c'est la fonction g qui est susceptible de correspondre à la fonction F.
2-
, donc la courbe représentative de g passe par le point de coordonnées (1,3).
et , donc .
.
Pour tout x de , , donc , donc , donc g est strictement croissante sur .
Pour tout x de , , donc , donc , donc g est strictement décroissante sur .
Il n'y a donc pas de contradiction avec les cinq informations énoncées en préambule en supposant que et .
Retour
|
|
|