| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 21 (enseignement de spécialité)
|
Enoncé.
Des touristes sont logés dans un hôtel noté A.
Un guide fait visiter six sites touristiques notés B, C, D, E, F et G.
Les tronçons de route qu'il peut emprunter sont représentés sur le graphe ci-dessous.
Le long de chaque arête figure la distance en kilomètres des différents tronçons.
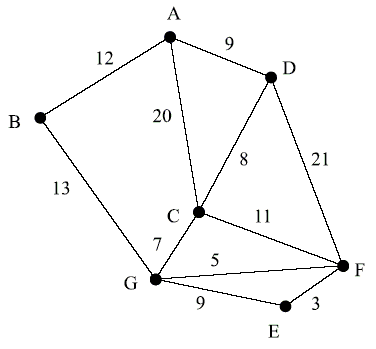
1- a) A partir de l'hôtel, le guide peut-il emprunter tous les tronçons de route en passant une et une seule fois sur chacun d'eux? Justifier la réponse.
b) Même question s'il doit obligatoirement terminer son circuit à l'hôtel.
2- Déterminer le plus court chemin menant de l'hôtel A au site E. Justifier la réponse.
Solution
1-a) A partir de l'hôtel, le guide peut emprunter tous les tronçons de route en passant une et une seule fois sur chacun d'eux. Il peut emprunter le chemin: ABGCADFEGFCD.
b) A partir de l'hôtel, si le guide doit emprunter tous les tronçons de route en passant une et une seule fois sur chacun d'eux et s'il doit obligatoirement terminer son circuit à l'hôtel, alors le chemin est un cycle eulérien. Le graphe défini ci-dessus est un graphe connexe qui n'a pas tous ses sommets de degré pair, donc il n'admet pas de cycle eulérien.
2- Le plus court chemin menant de l'hôtel A au site E est ADCFE de longueur 31 kilomètres.
Justification: Algorithme de Dijkstra:
| A |
B |
C |
D |
E |
F |
G |
| 0(A) |
12(A) |
20(A) |
9(A) |
|
|
|
| |
|
17(D) |
9(A) |
|
30(D) |
|
| |
|
17(D) |
|
|
28(C) |
24(C) |
| |
|
|
|
33(G) |
29(G) |
24(C) |
| |
|
|
|
31(F) |
28(C) |
|
| |
|
|
|
31(F) |
|
|
Dans le tableau on lit le plus court chemin de A à E de longueur 31. On lit les sommets dans l'ordre décroissant des distances à partir de E: EFCDA.
Retour
|
|
|