| Les sujets "zéro" du baccalauréat
|
| Série ES
|
| Exercice 22 (enseignement obligatoire)
|
Enoncé.
Un assembleur d'ordinateurs a équipé chacun d'eux d'une carte mère de marque, soit Elite, soit Futura. 35% des ordinateurs sont équipés de cartes mères Elite.
Il a aussi muni chacun d'eux d'un processeur choisi parmi trois références: Premium, P20 et P30.
- 60% des ordinateurs équipés de cartes mères Elite sont munis d'un processeur Premium et 30% d'un processeur P20.
- 30% des ordinateurs équipés de cartes mères Futura sont munis d'un processeur Premium et 20% d'un processeur P20.
On teste au hasard un ordinateur chez cet assembleur: tous les ordinateurs ont la même probabilité d'être testés.
On considère les événements suivants:
: "L'ordinateur est équipé d'une carte mère Elite"
: "L'ordinateur est équipé d'une carte mère Futura"
: "L'ordinateur est équipé d'un processeur Premium"
: "L'ordinateur est équipé d'un processeur P20"
: "L'ordinateur est équipé d'un processeur P30"
1- Construire un arbre pondéré décrivant la situation.
Dans les questions suivantes, les résultats des calculs seront arrondis au millième.
2- a) Déterminer la probabilité de l'événement .
b) Déterminer la probabilité de l'événement .
c) On teste au hasard un ordinateur équipé du processeur Premium. Quelle est la probabilité qu'il soit muni de la carte mère Futura?
3- L'assembleur gagne 450 ? sur un ordinateur équipé du processeur Premium, 250 ? sur un modèle équipé du processeur P20 et 120 ? sur un modèle équipé du processeur P30.
a) Déterminer la loi de probabilité du gain de l'assembleur.
b) Déterminer l'espérance mathématique de cette loi et interpréter le résultat.
Solution
1- Arbre pondéré décrivant la situation:
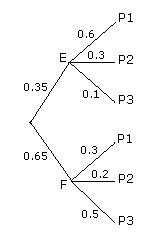
2- a)
b) Les événements E et F forment une partition de l'univers, donc d'après la formule des probabilités totales:
c) On veut calculer .
à 0.001 près.
3-a) La probabilité pour que l'assembleur gagne 450 ? est .
La probabilité pour que l'assembleur gagne 250? est .
La probabilité pour que l'assembleur gagne 120 ? est
La loi de probabilité du gain de l'assembleur est:
| Gain |
450 |
250 |
120 |
Total |
| Probabilité |
0.405 |
0.235 |
0.360 |
1 |
b)
L'espérance mathématique de la loi est donc 284.20 ?.
Cela signifie que si l'assembleur vend un grand nombre d'ordinateurs, alors en moyenne, son gain sera de 284.20 ?.
Retour
|
|
|