Maths.net

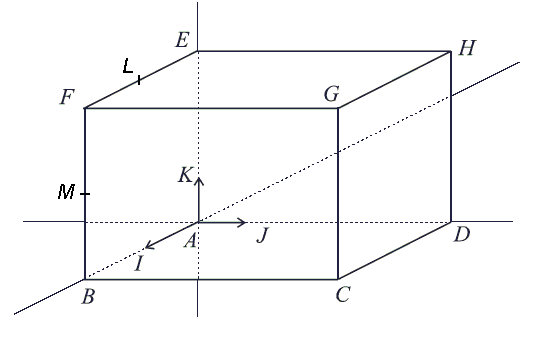
Les sujets "zéro" du baccalauréat Section ES Exercice 27 (enseignement de spécialité) Enoncé L'espace est rapporté à un repère orthonormal . Le parallélépipède rectangle ABCDEFGH est tel que: B(2,0,0), D(0,6,0), E(0,0,4). Les points L et M sont les milieux respectifs des segments [EF] et [FB]. 1- Placer les points L et M sur la figure ci-dessous. Donner (sans justification) les coordonnées des points A, C, F, G, H, puis vérifier par le calcul que les points L et M ont respectivement pour coordonnées (1,0,4) et (2,0,2). 2-Soit le plan d'équation: et le plan d'équation: a) Montrer que et ne sont pas parallèles. b) Soit l'intersection des deux plans et . Montrer que est la droite (ML). c) Justifier que le plan est parallèle à l'axe . 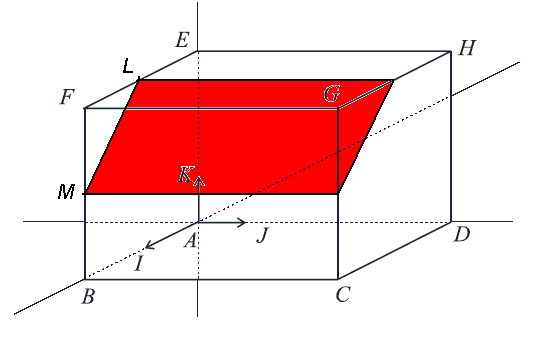d) Tracer en rouge sur la figure l'intersection de avec le pavé ABCDEFGH. On ne demande pas de justifier cette construction. Solution 1- Coordonnées des points: A(0,0,0), C(2,6,0), F(2,0,4), G(2,6,4), H(0,6,4). L est le milieu de [EF], donc les coordonnées de L sont la demi-somme des coordonnées de E et de F. On obtient . M est le milieu de [FB], donc les coordonnées de L sont la demi-somme des coordonnées de F et de B. On obtient 2- a) L'équation de est . L'équation de est . Les suites (0,1,0) et (2,0,1) ne sont pas proportionnelles, donc les plans ne sont pas parallèles. b) D'après le résultat ci-dessus, les deux plans sont sécants et se coupent suivant une droite. Les points L et M appartiennent au plan , puisque leur ordonnée est nulle. Les points L et M appartiennent au plan puisque et . Les points L et M appartiennent aux deux plans, donc la droite (LM) est la droite intersection des deux plans. c) L'équation de est , donc ce plan est parallèle à l'axe . d) L'intersection de avec le pavé ABCDEFGH est la figure tracée en jaune sur le graphique ci-dessous. Retour