Maths.net

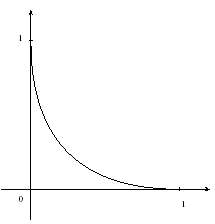
Les sujets "zéro" du baccalauréat Série S Exercice 4 (enseignement obligatoire) Enoncé Soit f la fonction définie sur l'intervalle [0,1] par . Cette fonction est dérivable sur ]0,1] et sa dérivée f' vérifie .La courbe représentative de la fonction f dans un repère orthonormal est donnée ci-contre. 1- (a) Montrer que le point M de coordonnées (x,y) appartient à si et seulement si , et . (b) Montrer que est symétrique par rapport à la droite d'équation . 2- (a) Si était un arc de cercle, quel pourrait être son centre? Quel pourrait être son rayon? (b) La courbe est-elle un arc de cercle? Solution 1- (a) Puisque x appartient au segment [0,1], alors . L'équation de est . Cette équation s'écrit: , donc . D'après l'équation ci-dessus, . Puisque x appartient au segment [0,1], alors , donc , donc . On en déduit: , donc . (b) L'équation de ci-dessus ne change pas si on échange les lettres x et y, donc si le point M de coordonnées (x,y) dans le repère orthonormal appartient à , alors le point de coordonnées (y,x), symétrique de M par rapport à la droite d'équation , appartient à .On en déduit que cette droite est axe de symétrie de la courbe . 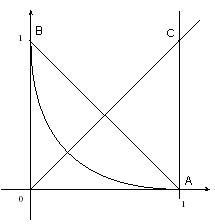2- (a) Si était un arc de cercle, alors son centre serait sur la médiatrice du segment [AB] (ci-contre). De plus, puisque , alors l'axe des abscisses est tangent à la courbe au point A, donc le centre du cercle serait sur la perpendiculaire en A à cet axe. On en déduit que le centre du cercle serait à l'intersection des deux droites, donc serait le point C de coordonnées (1,1). Dans ce cas le rayon serait égal à 1. (b) On considère le point de la courbe d'abscisse . Son ordonnée est . La distance de ce point au centre éventuel du cercle est le nombre: . Cette distance est différente de 1, le rayon supposé du cercle, donc un point de la courbe n'appartient pas au cercle supposé, donc la courbe n'est pas un arc de cercle. Retour