| Les sujets "zéro" du baccalauréat
|
| Série S
|
| Exercice 12 (enseignement obligatoire)
|
Enoncé
Le plan est rapporté à un repère orthonormal .
On note I le point de coordonnées (1,0).
Soient f la fonction définie sur l'intervalle [0,1] par et C sa courbe représentative dans le repère .
On note la portion de plan comprise entre la courbe C, l'axe des abscisses et les droites d'équations x=0 et x=1.
Le but de l'exercice est de prouver l'existence d'un unique réel appartenant à l'intervalle [0,1] tel que, si A est le point de C d'abscisse , le segment [IA] partage en deux régions de même aire.
Pour tout x appartenant à l'intervalle [0,1], on note le point de coordonnées (x,f(x)) et le domaine délimité par la droite , l'axe des abscisses, l'axe des ordonnées et la courbe C.
On désigne par g(x) l'aire de .
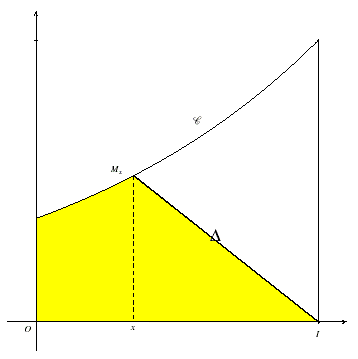
1- Pour tout x appartenant à l'intervalle [0,1], calculer g(x) en fonction de x.
2- Etudier les variations de la fonction g qui à x associe g(x) sur [0,1].
3-(a) Par des considérations d'aires, montrer que .
(b) Montrer qu'il existe un unique réel de [0,1] tel que soit égal à la moitié de l'aire de .
4-Trouver une valeur approchée de à 0.001 près par défaut.
Solution
1- Pour tout x appartenant à l'intervalle [0,1], g(x) est la somme de l'aire du domaine délimité par la courbe C, l'axe des abscisses, l'axe des ordonnées et la droite d'équation t=x et l'aire du triangle délimité par la droite , l'axe des abscisses et la droite d'équation t=x.
Une primitive de f sur [0,1] est la fonction F définie par: , donc:
2-
Pour tout x de [0,1], et , donc .
On en déduit que la fonction g est strictement croissante sur [0,1].
3-(a)
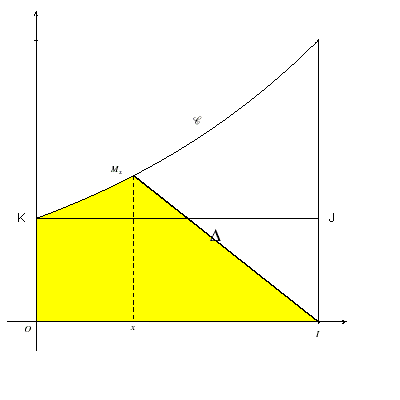
g(0) est l'aire du triangle OIK, donc est l'aire du rectangle OIJK.
est l'aire de la portion de plan .
Comme le rectangle est inclus dans alors , donc .
(b) est l'aire de .
La fonction g est continue et strictement croissante sur [0,1], est inférieur à la moitié de l'aire de et est supérieur à la moitié de l'aire de , donc il existe un unique réel de [0,1] tel que soit égal à la moitié de l'aire de .
4-Une valeur approchée de à 0.001 près par défaut est 0.331.
Retour
|
|
|