| Les sujets "zéro" du baccalauréat
|
| Série S
|
| Exercice 18 (enseignement obligatoire)
|
Enoncé
On sait tous qu'il y a des années à coccinelles et d'autres sans!
On se propose d'étudier l'évolution d'une population de coccinelles à l'aide d'un modèle utilisant la fonction numérique f définie par , k étant un paramètre qui dépend de l'environnent (k appartient à ).
Dans le modèle choisi, on admet que le nombre des coccinelles reste inférieur à un million.
L'effectif des coccinelles, exprimé en millions d'individus, est approché pour l'année n par un nombre réel , avec compris entre 0 et 1. Par exemple, si pour l'année zéro il y a 300 000 coccinelles, on prendra .
On admet que l'évolution d'une année sur l'autre obéit à la relation , f étant la fonction définie ci-dessus.
Le but de l'exercice est d'étudier le comportement de la suite pour différentes valeurs de la population initiale et du paramètre k.
1- Démontrer que si la suite converge, alors sa limite l vérifie la relation .
2- Supposons et .
(a) Etudier le sens de variation de la suite .
(b) Montrer par récurrence que, pour tout entier n,
.
(c) La suite est-elle convergente? Si oui, quelle est sa limite?
(d) Que peut-on dire de l'évolution à long terme de la population de coccinelles avec ces hypothèses?
3- Supposons maintenant et .
(a) Etudier les variations de la fonction f sur [0,1] et montrer que appartient à .
(b) En utilisant éventuellement un raisonnement par récurrence,
- montrer que, pour tout entier naturel n,
;
- établir que, pour entier naturel n, .
(c) La suite est-elle convergente? Si oui, quelle est sa limite?
(d) Que peut-on dire de l'évolution à long terme de la population de coccinelles avec ces hypothèses?
4- On a représenté dans les annexes la fonction f dans les deux cas étudiés ci-dessus ainsi que la droite d'équation y=x. Le troisième graphique correspond au cas où et k=3.2.
Illustrer sur les deux premiers graphiques les résultats trouvée en 1. et 2. en laissant les traits de construction et en faisant apparaître en abscisse les valeurs successives , ,, ...
En utilisant la même méthode, formuler une conjecture sur l'évolution de la population dans le troisième cas.
Annexes
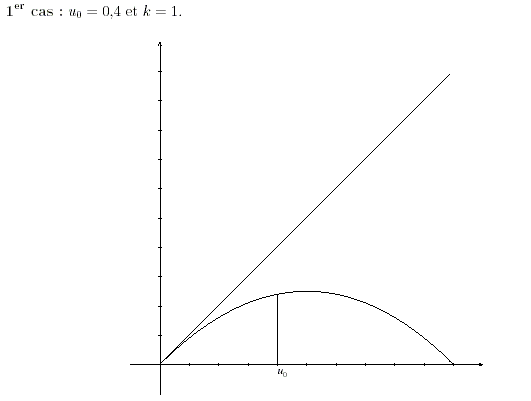
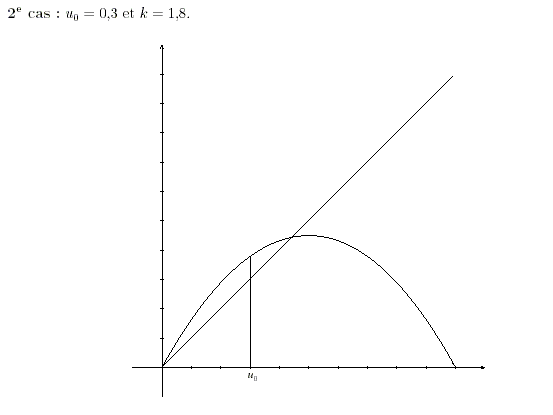
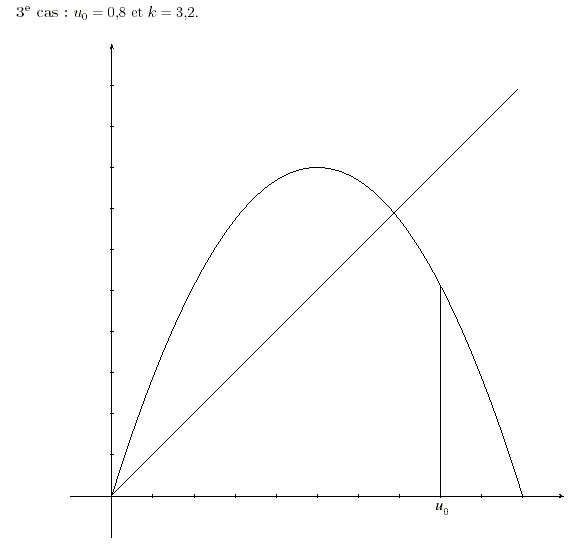
Solution
1- La suite est définie par la relation de récurrence: Pour tout entier naturel n, , f étant la fonction définie par: .
f est continue en tout x de donc, si la suite converge vers l, alors .
2- (a) On suppose et , donc pour tout entier naturel n, .
Pour tout entier naturel n, est inférieur ou égal à 0, donc . On en déduit que la suite est décroissante.
(b)
- , donc
.
- Tableau de variation de la fonction f sur [0,1]:
D'après le tableau ci-dessus, pour tout x de [0,1], f(x) est compris entre 0 et .
Donc si on suppose compris entre 0 et 1, alors puisque , alors est compris entre 0 et 1.
- D'après les deux résultats ci-dessus alors pour tout n, est compris entre 0 et 1.
(c) La suite est croissante et majorée par 1, donc elle est convergente. La limite l de la suite est telle que .
On obtient:
La limite de la suite est 0.
(d) Avec ces hypothèses, à long terme, la population de coccinelles diminue en se rapprochant de 0.
3- (a) On suppose et , donc pour tout entier naturel n, .
Tableau de variation de la fonction f sur [0,1]:
D'après le tableau ci-dessus, , donc appartient à .
(b)
- , donc
.
- D'après (a), si on suppose compris entre 0 et , alors puisque , alors est compris entre 0 et , donc entre 0 et .
- D'après les deux résultats ci-dessus, pour tout n, alors est compris entre 0 et .
- , donc .
-
Puisque pour tout n, est compris entre 0 et alors est compris entre 0 et 1; donc, est compris entre 0 et 1.
On en déduit que est de même signe que .
D'après les deux résultats ci-dessus: pour entier naturel n, .
(c) D'après 3- (b) la suite est croissante et majorée par , donc elle est convergente.
Sa limite l est telle que . On obtient: , donc ou .
Puisque la suite est croissante et de premier terme 0.3, alors sa limite ne peut être 0, donc elle est égale à .
(d) Des résultats ci-dessus on déduit qu'avec ces hypothèses, à long terme, la population de coccinelles augmente en se rapprochant de millions d'individus.
4- Le graphique ci-dessous illustre les résultats trouvés en 1-.
Le graphique ci-dessous illustre les résultats trouvés en 2-.
Le graphique ci-dessous correspond au cas où et .
Graphiquement on peut supposer que la suite a pour limite l'abscisse du point d'intersection de la courbe représentative de f et de la droite d'équation y=x.
Cette limite l, différente de 0, est telle que .
On obtient .
Retour
|
|
|