| Les sujets "zéro" du baccalauréat
|
| Série S
|
| Exercice 29 (enseignement de spécialité)
|
Enoncé
Des nombres étranges!
Les nombres 1;11;111;1111; etc. sont des nombres que l'on appelle rep-units (répétitions de l'unité). Ils ne s'écrivent qu'avec des chiffres 1. Ces nombres possèdent de nombreuses propriétés qui passionnent des mathématiciens.
Cet exercice propose d'en découvrir quelques-unes.
Pour k, entier strictement positif, on note le rep-unit qui s'écrit à l'aide de k chiffres 1.
Ainsi , ,,...
1- Citer deux nombres premiers inférieurs à 10 n'apparaissant jamais dans la décomposition d'un rep-unit.
Justifier brièvement la réponse.
2- A quelle condition sur k le nombre 3 apparaît-il dans la décomposition du rep-unit ?
Justifier brièvement la réponse.
3- Pour , le rep-unit est défini par .
Justifier l'égalité: pour tout entier k supérieur ou égal à 1.
4- Le tableau ci-dessous donne les restes de la division par 7 de , pour k entier compris entre 1 et 8.
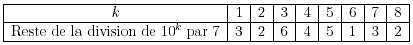
Soit k un entier strictement positif. Démontrer que:
"
(7)" équivaut à "k est multiple de 6".
En déduire que 7 divise si, et seulement si k est multiple de 6.
Solution
1- 2 en fait partie, car un rep-unit est impair.
5 en fait partie car un rep-unit ne finit ni par un 0, ni par un 5.
2- Un entier est divisible par 3 si et seulement si la somme de ses chiffres est divisible par 3. La somme des chiffres d'un rep-unit est k; donc est divisible par 3 si et seulement si k est divisible par 3.
3- Soit une suite définie sur par . est une suite géométrique de raison 10 et de premier terme 1, donc pour tout n appartenant à :
donc
donc .
4- Soit k un entier non nul. On a:
. Or d'après le tableau, s'écrit sous la forme . Donc:
soit
soit
donc:
[7].
Soit k un entier non nul tel que [7]. Montrons que k est multiple de 6. Si k est inférieur ou égal à 6, d'après le tableau, k=6, donc k est multiple de 6.
Supposons que k est strictement supérieur à 6, et écrivons la division euclidienne de k par 6. On sait que:
[7] soit
[7] soit
[7].
Or d'après la démonstration ci-dessus, on peut écrire sous la forme . Donc:
[7] soit
[7] donc
[7].
Or q étant le reste de la division euclidienne de k par 6, q est compris entre 0 et 5. D'après le tableau, on a nécessairement q=0. Donc k est divisible par 6. L'équivalence est donc prouvée. CQFD!
Retour
|
|
|