| Algèbre
|
| Equations à une inconnue, du premier degré ou s'y ramenant
|
| Exercice 21
|
Résoudre l'équation d'inconnue réelle x.
Rédaction
|
|
Commentaires
|
| __________________________________________________________________________________________________________
|
Ligne 1
L'équation contient l'inconnue dans deux dénominateurs, dans l'ordre: et .
Le premier dénominateur est nul si .
Le second dénominateur est nul si .
Donc toute solution de l'équation doit être différente de et de .
|
Lorsque l'équation contient un dénominateur contenant l'inconnue x, toute valeur a de x qui annule ce dénominateur est à exclure et ne peut être solution de l'équation.
Si l'équation contient un dénominateur qui ne contient pas x, alors il est constant et ne peut être nul.
La barre de fraction du premier membre signifie qu'il faut diviser par le nombre du dénominateur.
Dans ce cas le dénominateur est égal à 0 pour la seule valeur -2 de x, donc le nombre -2 ne peut être solution de l'équation.
La barre de fraction du second membre signifie qu'il faut diviser par le nombre du dénominateur.
Dans ce cas le dénominateur est égal à 0 pour la seule valeur 2 de x, donc le nombre 2 ne peut être solution de l'équation.
|
| __________________________________________________________________________________________________________
|
Ligne 2
L'équation est du type (avec b différent de 0 et d différent de 0), ce qui équivaut à:
.
On obtient donc:
On développe les deux membres:
On réduit les deux membres:
On rassemble les termes en x dans le premier membre et les termes constants dans le second:
Pour toute valeur a de x l'égalité est , donc la valeur a n'est pas de l'équation.
L'ensemble des solutions de l'équation est l'ensemble .
|
L'égalité (avec b différent de 0 et d différent de 0) équivaut à .
En français: le produit des extrêmes est égal au produit des moyens.
On dit aussi que les produits en croix sont égaux.
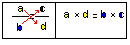
En regroupant les termes en x dans le premier membre on constate qu'ils s'annulent. Le second membre étant différent de 0, alors, pour tout réel, l'égalité ne peut être vraie. Donc l'équation n'a pas de solution.
|
Retour
|
|
|